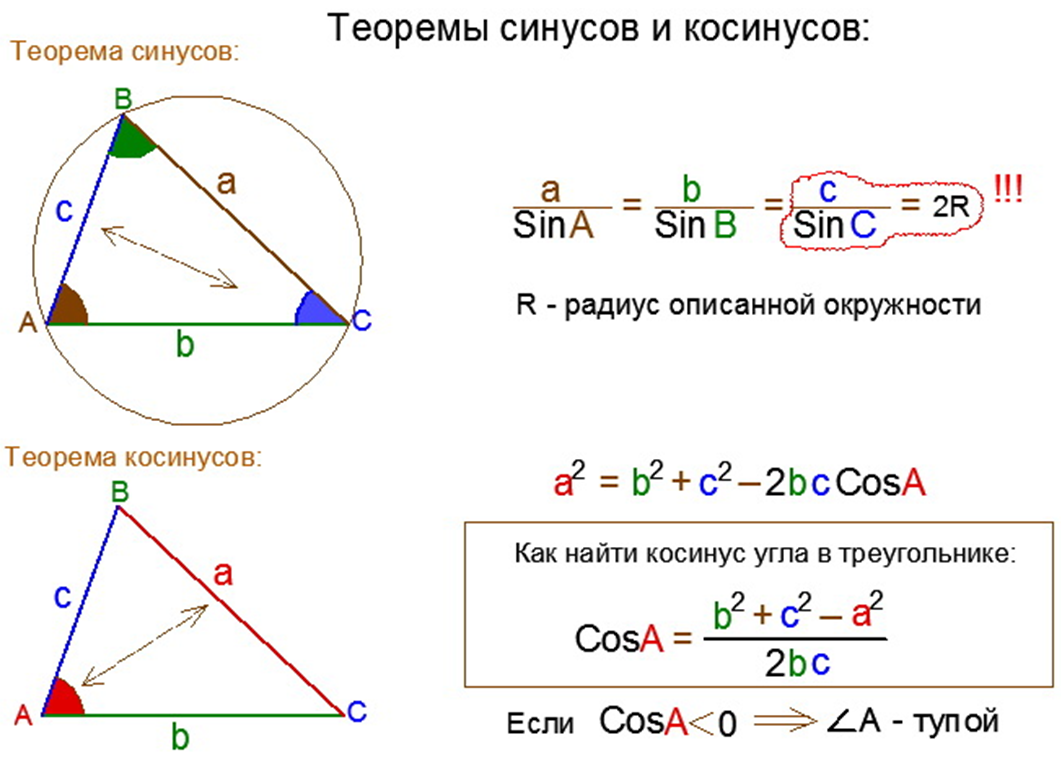
Теорема косинусов для треугольника задания - Универсальный справочник

Теорема косинусов

Для любого треугольника справедливо следующее соотношение:

( a^2=b^2+c^2-2 cdot b cdot c cdot cos ;; alpha )

Квадрат стороны треугольника равен сумме квадратов двух других сторон вычесть удвоенное произведение
этих сторон на косинус угла между ними.

Кликнув по этому тексту мы сразу перейдем
к задачам на нахождение угла по трем сторонам треугольника, используя теорему косинусов

Репетитор по геометрии, физике и математике

8 916 478 10 32

Простейшие задачи на теорему косинусов:

Задача 1. (Решить задачу, применив теорему косинусов)

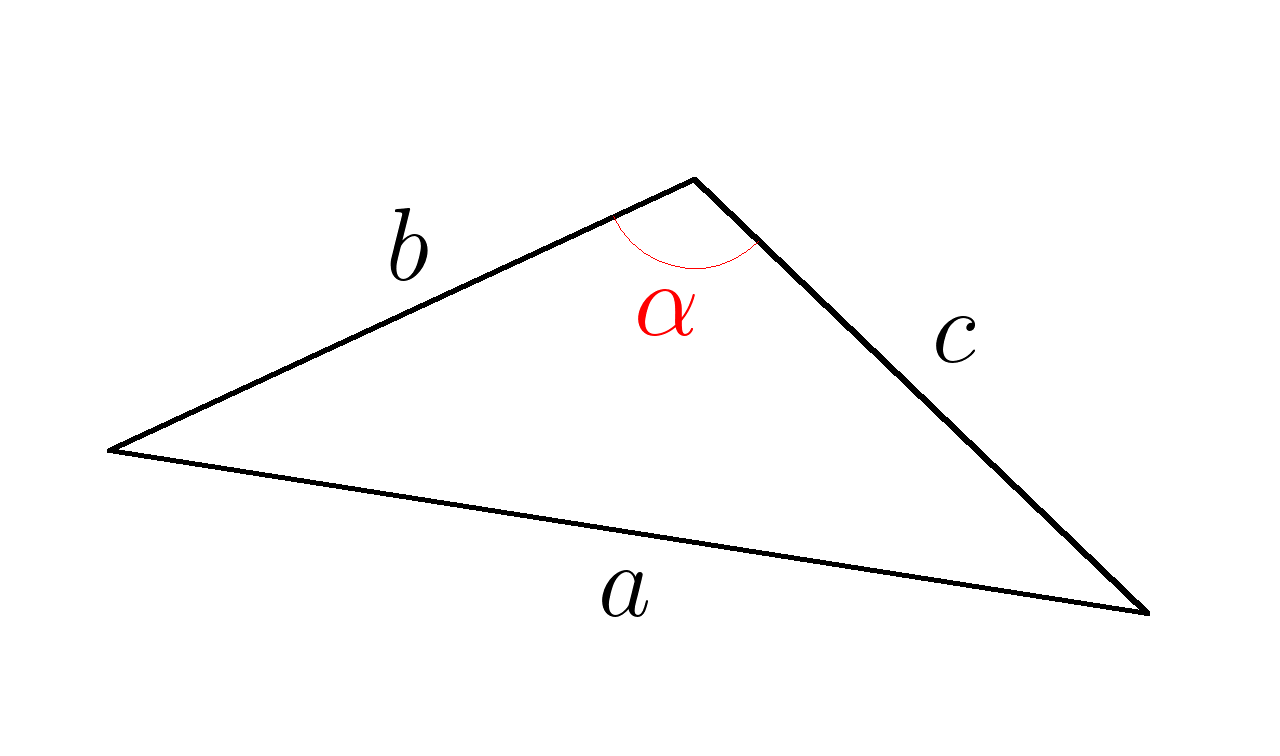
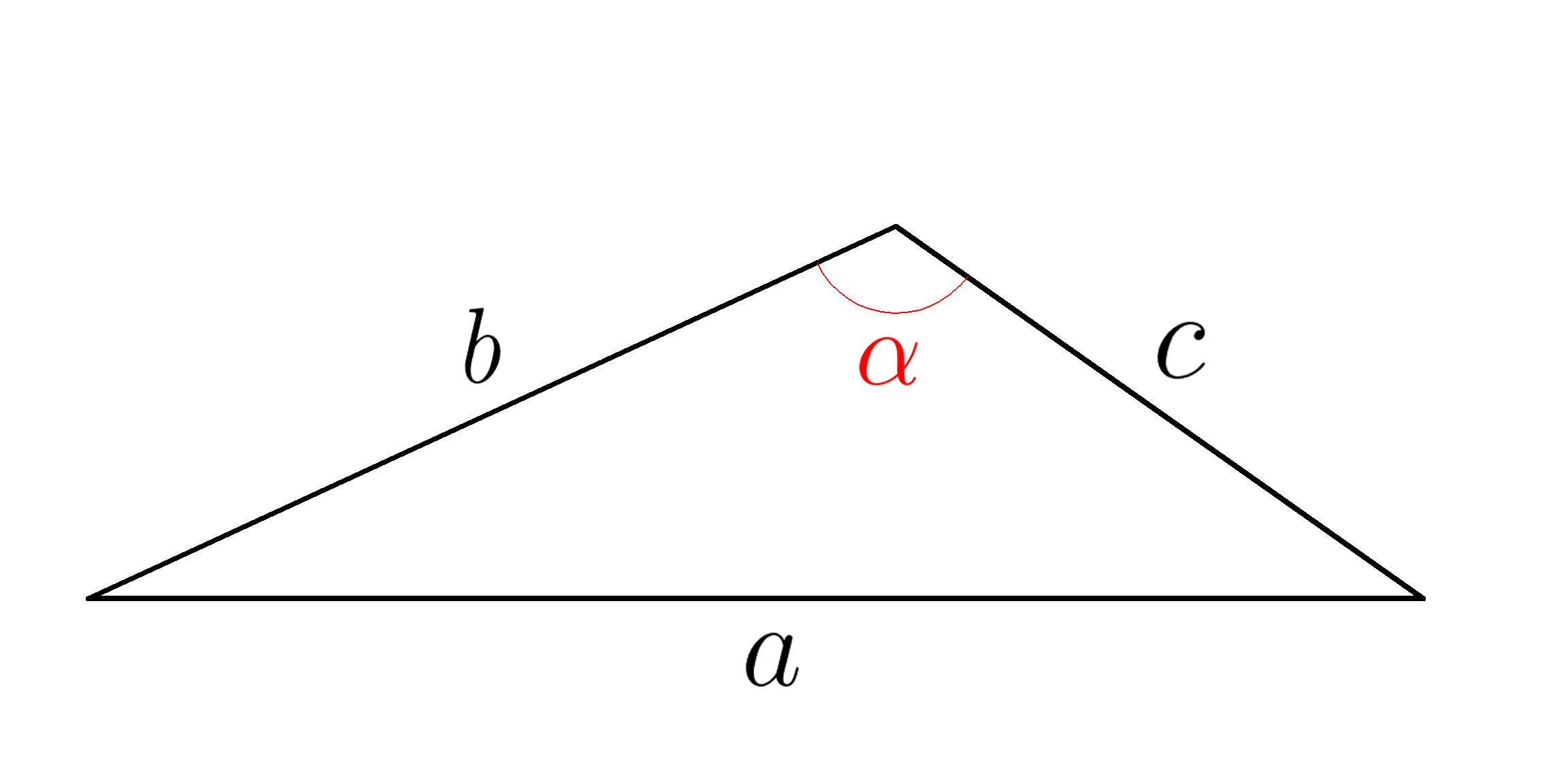
В треугольнике, изображенном на рисунке ( b=7 , c=15, alpha=60^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение

Репетитор по геометрии

8 916 478 10 32

Задача 2. (Решить задачу, применив теорему косинусов)



В треугольнике, изображенном на рисунке ( b=3 , ; c=8, ; alpha=60^0 ,; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение

Задача 3. (Решить задачу, применив теорему косинусов)

В треугольнике, изображенном на рисунке ( b=6 , ; c=16, ; alpha=60^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение



4. В треугольнике, изображенном на рисунке ( b=2 , ; c=sqrt{3}, ; alpha=30^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение



5. В треугольнике, изображенном на рисунке ( b=4 , ; c=2sqrt{3}, ; alpha=30^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение



6. В треугольнике, изображенном на рисунке ( a=13 , c=15, alpha=60^0 , ; ) найти сторону (b . )
Показать ответ
Показать решение
Видеорешение



7. В треугольнике, изображенном на рисунке (a=7, ; b=3 , ; alpha=60^0 , ; ) найти сторону (c . )
Показать ответ
Показать решение
Видеорешение



8. В треугольнике, изображенном на рисунке (a=14, ; b=6 , ; alpha=60^0 , ; ) найти сторону (c . )
Показать ответ
Показать решение
Видеорешение



9. В треугольнике, изображенном на рисунке (a=1, ; c=sqrt{3} , ; alpha=30^0 , ; ) найти сторону (b . )
Показать ответ
Показать решение
Видеорешение



15. В треугольнике, изображенном на рисунке ( b=4 , c=2+sqrt{37}, alpha=60^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение



16. В треугольнике, изображенном на рисунке ( b=5sqrt{2} , c=5+sqrt{11}, alpha=30^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение

Задача 20. (Решить задачу, применив теорему косинусов)



В треугольнике, изображенном на рисунке ( b=35 , c=21, alpha=120^0 , ; ) найти сторону (a . )
Показать ответ
Показать решение
Видеорешение

Задачи на нахождение угла по трем сторонам треугольника
с применением теоремы косинусов

Задача 22. (Решить задачу, применив теорему косинусов)



В треугольнике, изображенном на рисунке (a=13, b=7 , c=15 , ; ) найти угол (alpha . )
Показать ответ
Показать решение
Видеорешение

Задача 23. (Решить задачу, применив теорему косинусов)



В треугольнике, изображенном на рисунке (a=7, b=3 , c=8 , ; ) найти угол (alpha . )
Показать ответ
Показать решение
Видеорешение

Источник

СДАМ ГИА: РЕШУ УРОК

Сайт в разработке

Планиметрия

планиметрия

Алгебра

Анализ

Планиметрия

Стереометрия

Экзамены

Физика 7–9

Физика 10–11

сайты — меню — вход — новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Каталог заданий

Ученику

Учителю

Школа

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Новости

31 января

Внедрили тёмную тему!

15 декабря

Новый раздел: выпускные экзамены

8 апреля

Математика необычного телеурок Д. Д. Гущина на телеканале 78

Все новости

Каталог заданий.
Теорема косинусов

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 30 № 1120

Определите вид треугольника по длинам его сторон: 5, 8 и 10.

Аналоги к заданию № 1120: 1121 1122 1123 Все

Решение

Помощь

Тип 30 № 1121

Определите вид треугольника по длинам его сторон: 4, 5 и 6.

Аналоги к заданию № 1120: 1121 1122 1123 Все

Решение

Помощь

Тип 30 № 1122

Определите вид треугольника по длинам его сторон: 7, 24 и 25.

Аналоги к заданию № 1120: 1121 1122 1123 Все

Решение

Помощь

Тип 30 № 1123

Определите вид треугольника по длинам его сторон: 16, 63 и 65.

Аналоги к заданию № 1120: 1121 1122 1123 Все

Решение

Помощь

Тип 30 № 1124

Определите вид треугольника, если его стороны относятся как 2:3:4.

Аналоги к заданию № 1124: 1125 Все

Решение

Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Геометрия 7-9 класс. Теорема косинусов

Геометрия 7-9 класс. Теорема косинусовadmin2022-12-27T10:00:24+03:00

Скачать файл в формате pdf.

Геометрия 7-9 класс. Теорема косинусов

Задача 1. В треугольнике АВС АВ = 5, АС = 8 и (angle ,A = {60^ circ }.) Найдите ВС.

Ответ

ОТВЕТ: 7.

Задача 2. В треугольнике АВС (AB = 2sqrt 7 ,,,,AC = sqrt 7 ) и (angle ,A = {120^ circ }.) Найдите ВС.

Ответ

ОТВЕТ: 7.

Задача 3. В треугольнике АВС АВ = 10, АС = 16 и ВС = 14. Найдите угол А. Ответ дайте в градусах.

Ответ

ОТВЕТ: 60.

Задача 4. В треугольнике АВС (AB = sqrt {13} ,,,,AC = 3sqrt {13} ,,) ВС = 13. Найдите угол А. Ответ дайте в градусах.

Ответ

ОТВЕТ: 120.

Задача 5. В треугольнике со сторонами 4, 6 и 8 найдите косинус наибольшего угла.

Ответ

ОТВЕТ: — 0,25.

Задача 6. В треугольнике со сторонами 4, 6 и 8 найдите косинус наименьшего угла.

Ответ

ОТВЕТ: 0,875.

Задача 7. Стороны параллелограмма равны 3 и 4, а одна из диагоналей (sqrt {34} .) Найдите вторую диагональ.

Ответ

ОТВЕТ: 4.

Задача 8. Диагонали параллелограмма равны (sqrt {32} ) и (sqrt {72} ,) а одна из сторон равна 6. Найдите периметр параллелограмма.

Ответ

ОТВЕТ: 20.

Задача 9. В треугольнике со сторонами 4, 13 и 15 найдите наибольшую высоту треугольника.

Ответ

ОТВЕТ: 12.

Задача 10. В треугольнике со сторонами 13, 14 и 15 найдите среднюю по величине высоту треугольника.

Ответ

ОТВЕТ: 12.

Задача 11. В четырёхугольнике ABCD АВ = 5, ВС = 3, (AD = sqrt 3 ,) (angle ,B = {60^ circ }) и (angle ,D = {90^ circ }.) Найдите CD.

Ответ

ОТВЕТ: 4.

Задача 12. В четырёхугольнике ABCD АВ = 4, ВС = 5, AD = 6, (angle ,B = {120^ circ }) и (angle ,D = {90^ circ }.) Найдите CD.

Ответ

ОТВЕТ: 5.

Задача 13. В треугольнике АВС АВ = ВС = 4. Найдите АС, если медиана АМ = 3. В ответ запишите (A{C^2}.)

Ответ

ОТВЕТ: 10.

Задача 14. В треугольнике АВС АВ = 5, ВС = 12. На стороне ВС выбрана точка М так, что ВМ : МС = 1 : 2. Найдите АС, если (AM = 5sqrt 2 .)

Ответ

ОТВЕТ: 14.

Задача 15. Площадь треугольника АВС равна (10sqrt 3 .) Найдите периметр этого треугольника, если ВС = 8 и (angle ,B = {60^ circ }.)

Ответ

ОТВЕТ: 20.

Задача 16. Площадь треугольника АВС равна (frac{{15sqrt 3 }}{4}.) Найдите периметр этого треугольника, если ВС = 5 и (angle ,B = {120^ circ }.)

Ответ

ОТВЕТ: 15.

Задача 17. В треугольнике со сторонами 2, 3 и (sqrt {10} ) найдите меньшую из трёх медиан.

Ответ

ОТВЕТ: 2.

Задача 18. В треугольнике АВС АВ = 3, АС = 5 и медиана (AM = sqrt {13} .) Найдите ВС.

Ответ

ОТВЕТ: 4.

Задача 19. В треугольнике АВС АВ = 9, ВС = 6 и (angle ,B = {60^ circ }.) Найдите радиус описанной окружности треугольника АВС.

Ответ

ОТВЕТ: (sqrt {21} .)

Задача 20. Радиус окружности, описанной около треугольника АВС, равен (sqrt {39} .) Найдите ВС, если АВ = 9 и (angle ,B = {60^ circ }.)

Ответ

ОТВЕТ: 12.

Задача 21. В четырёхугольник ABCD можно вписать окружность. Найдите сумму сторон ВС и CD, если АВ = 5, AD = 12, (angle ,A = {90^ circ }) и (angle ,C = {60^ circ }.)

Ответ

ОТВЕТ: 23.

Задача 22. В четырёхугольник ABCD можно вписать окружность и около него можно описать окружность. Найдите сумму сторон ВС и CD, если АВ = 3, AD = 2 и (angle ,A = {60^ circ }.)

Ответ

ОТВЕТ: 3.

Задача 23. В треугольнике АВС АВ = 10, (BC = 3sqrt 2 ), СМ – медиана. Найдите площадь треугольника АВС, если (angle ,MCB = {45^ circ }.)

Ответ

ОТВЕТ: 21.

Задача 24. В параллелограмме ABCD угол А тупой. Найдите диагональ BD, если периметр параллелограмма равен 18, площадь – 16, а (sin A = frac{4}{5}.)

Ответ

ОТВЕТ: (sqrt {65} .)

Источник

Инфоурок

›

Алгебра

›Другие методич. материалы›Задачи на теорему синуса, косинуса и площадь треугольника

Задачи на теорему синуса, косинуса и площадь треугольника

Скачать материал

Сейчас обучается 141 человек из 50 регионов

Сейчас обучается 23 человека из 12 регионов

Сейчас обучается 105 человек из 33 регионов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 212 128 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

Презентация по алгебре 7 класс

Учебник: «Алгебра», Мерзляк А.Г., Полонский В.Б., Якир М.С.
Тема: § 9. Сложение и вычитание многочленов

31.01.2019
617
11

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
Курс профессиональной переподготовки «Клиническая психология: организация реабилитационной работы в социальной сфере»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
Курс повышения квалификации «Информационная этика и право»
Курс профессиональной переподготовки «Управление качеством»

Скачать материал
- 31.01.2019
  
  18960
- DOCX
  39 кбайт
- 856
  скачиваний
- Рейтинг:
  5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Лаптева Евгения Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 6 лет и 6 месяцев
- Подписчики: 7
- Всего просмотров: 83371
- Всего материалов:
  
  75

Источник

Теорема косинусов отлично помогает в решении треугольников. Решение треугольника – это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 90⁰.

Теорема и доказательство

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательство теоремы косинусов

Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:

Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:

В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:

$[overrightarrow{BC}^2=overrightarrow{AB}^2+overrightarrow{AC}^2-2overrightarrow{AB}cdot overrightarrow{AC} eqno (2)]$

Так как, $overrightarrow{BC}^2={BC}^2$ , $overrightarrow{AC}={AC}^2$ , а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть .

Подставим все в формулу (2):

Что и требовалось доказать.

Следствие теоремы косинусов

Проведем высоты :

Обратим внимание, что . То есть – это проекция стороны на сторону треугольника . Если угол А острый, то , если угол А тупой, то косинус угла А будет отрицательным и . То есть из теоремы косинусов вытекает важное следствие:

квадрат стороны треугольника равен сумме квадратов двух других сторон “” удвоенное произведение одной из них на проекцию другой на эту сторону. Знак надо брать, если угол тупой, а знак , если угол острый.

Задачи на теорему косинусов

Задача 1

Найдите , если дано: $angle B = 60^{circ}$ , , .

Решение: Так как нам известен угол между сторонами и и известна сторона – мы сможем найти сторону , если воспользуемся теоремой косинусов.

Из теоремы косинусов $AC^2={AB}^2+{BC}^2-2AB cdot {BC} cos {angle B}$ выразим сторону .

Получим:

${BC}^2-2AB cdot {BC} cos {angle B}-AC^2+{AB}^2 = 0$

Обозначим

Тогда

$x^2-2AB cdot cos {angle B} cdot x-AC^2+{AB}^2=0$

Получаем квадратное уравнение. Подставим в него значения и решим:

$x^2-2 cdot 8 cdot frac{1}{2} x-{(4 sqrt 7)}^2+8^2=0$

Находим дискриминант:

Тогда $x_1=frac{8+16}{2}=frac{24}{2}=12$ .

$x_2=frac{8-16}{2}=frac{-8}{2}=-4$ – не может быть длиной стороны треугольника.

Ответ: 12.

Задача 2

В треугольника ABC , $angle C=120^{circ}$ , . Найдите

Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.

Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:

$[AB^2={AC}^2+{BC}^2-2AC cdot {BC} cos {angle 120^{circ}} eqno (1)]$

Так как , то из формулы (1), получим:

$AB^2=2{AC}^2-2{AC}^2 cdot cos {angle 120^{circ}}$

Сделаем замену: :

$AB^2=2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}$ ,

перенесем ${AB}^2$ в правую часть равенства и получим квадратное уравнение:

$2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{AB}^2=0$ ,

Подставим значения:

$2{x}^2-2{x}^2 cdot cos {angle 120^{circ}}-{(6sqrt{3})}^2=0$

$cos {angle 120^{circ}}=-frac{1}{2}$

$2{x}^2+{x}^2-108=0$

$3{x}^2=108$

${x}^2=36$

Так как , значит, .

Ответ: 6

Задача 3

Решите треугольник ABC, если известно, что $angle A=30^{circ}$ , , $angle C=45^{circ}$ .

Решение: Решить треугольник – это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна $180^{circ}$ получим:

$angle B = 180^{circ}-30^{circ}-45^{circ}=105^{circ}$ .

Обозначим неизвестные стороны треугольника: , .

Выразим сторону треугольник по теореме косинусов:

$[AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}eqno (1)]$

Выразим сторону треугольника по теореме косинусов:

$y^2={x}^2+{AB}^2-2{x}cdot{AB} cdot cos {30^{circ}}$

или

$[y^2={x}^2+16-8{x}cdot cos {30^{circ}} eqno (2)]$

Решим уравнения (1) и (2) совместно, записав их в систему уравнений:

$[left{ begin{aligned} AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}\ y^2={x}^2+16-8{x}cdot cos {30^{circ}}.\ end{aligned} right.]$

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ y^2={x}^2+16-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Преобразуем второе уравнение системы:

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ -16={x}^2-y^2-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:

$[left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ 0=2{x}^2-xy sqrt{2}-4{x}cdot sqrt{3}.\ end{aligned} right.]$

Из второго уравнения выразим :

$xy sqrt{2}=2x^2-4x sqrt{3}$

$y=frac{2x^2-4x sqrt{3}}{x sqrt{2}}$

$y=frac{2x-4sqrt{3}}{sqrt{2}}$

Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.

$16=x^2+(frac{2x-4sqrt{3}}{sqrt{2}})^2-x sqrt{2}(frac{2x-4sqrt{3}}{sqrt{2}})$ , раскрываем скобки и умножим левую и правую части уравнения на 2:

$32=2x^2+4x^2-16x sqrt{3}+16 cdot 3-2x(2x-4 sqrt{3})$

$2x^2-8x sqrt{3}+48-32=0$

$2x^2-8x sqrt{3}+16=0$

Разделим левую и правую части уравнения на 2:

$x^2-4x sqrt{3}+8=0$ .

Получили квадратное уравнение. Решим его.

Находим дискриминант:

$D=b^2-4ac=(4 sqrt{3})^2-4 cdot 8 cdot 1=16 cdot 3 - 32=48-32=16$

Тогда корни уравнения:

$x_1=frac{-b-sqrt{D}}{2a}=frac{4 sqrt{3}-4}{2}=2 sqrt{3}-2$

$x_2=frac{-b+sqrt{D}}{2a}=frac{4 sqrt{3}+4}{2}=2 sqrt{3}+2$ .

Оба значения подходят – они положительны. Находим, :

$y_1= frac{2(2 sqrt{3}-2)-4 sqrt{3}}{sqrt{2}}=frac{-4}{sqrt{2}}$ – отрицательное значение нам не подходит.

$y_2= frac{2(2 sqrt{3}+2)-4 sqrt{3}}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ .

Таким образом, получаем следующие значения , .

Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.

Ответ: , .

Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему – синусов. Например, третью задачу мы могли решить гораздо проще – используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение . Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы – рекомендуем решать задачи, используя их обе.

Источник

Теорема косинусов

Геометрия 7-9 класс. Теорема косинусов

Геометрия 7-9 класс. Теорема косинусов

Задачи на теорему синуса, косинуса и площадь треугольника

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Теорема и доказательство

Теорема косинусов

Доказательство теоремы косинусов

Следствие теоремы косинусов

Задачи на теорему косинусов

Задача 1

Задача 2

Задача 3

Добавить комментарий Отменить ответ