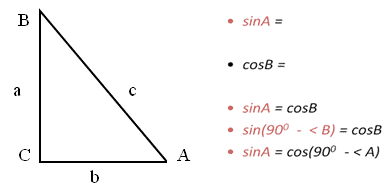Теорема косинусов для треугольника какой класс - Универсальный справочник

Изучение темы «Теорема косинусов» в 9-ом
классе.

Цели уроков:

Образовательные:
- усвоение всеми учащимися стандартного минимума
  по теме;
- формирование и совершенствование
  надпредметных умений обобщать путем
  сравнения, постановка и решение проблем,
  оперирование уже знакомыми геометрическими
  понятиями и фактами, рассуждение по аналогии;
- развитие психологических характеристик
  личности учащихся: способности к
  абстрагированию, выдвижению гипотез,
  формулированию проблем;
- развитие психических свойств: память,
  вербальная и образная, произвольное внимание,
  воображение.
Развивающие:
- определение зоны ближайшего развития учащихся
  в ходе решения задач с использованием теоремы
  косинусов;
- определение результативности и
  эффективности подготовительного этапа урока к
  доказательству теоремы косинусов через
  анализ и обобщение домашней работы;
- определение возможности конструирования
  познавательного процесса.

Начало урока. Организационный момент
устанавливает личностный контакт учителя с
учениками через формирование целей урока, их
взаимного принятия и включение мотива на
совместную работу. Положительная мотивация
достигается анализом успешной работы учащихся с
теоремой синусов и ее применением к решению
задач.

Этап подготовки к осознанному восприятию
нового материала

1. (Ученик 1). Рассказ о косинусе
угла:

определение;
значения косинусов некоторых углов от 0о до 180о;
свойство косинусов равных углов;
свойство косинусов смежных углов;
свойство косинусов углов, значения которых
увеличиваются о 0^о до 90^о.

2. (Ученик 2) Приложение.
Слайд 2.

Задание: Используя
треугольник АВС, найдите синус угла А и
косинус угла А.Сделайте вывод.

Замечание. Острые углы А и В
прямоугольного треугольника АВС дополняют друг
друга. 90^о и являются дополнительными.

Вывод: Косинус острого угла равен
синусу дополнительного угла.

3. (Ученик 3) Используя
четырехзначные математические таблицы Брадиса,
найдите

1) cos25^о;
2) угол , если cos = 0,4756;
    cos25^о15′;
       cos = 0,5638;
    cos25^о18′;
                                                                                  cos = 0,8975.
    сos43^о39′.

4. Анализ и обсуждение домашнего
задания. Слайд 3.

1) (Ученик 4) Задача 1.
Постройте угол, если его
а) синус угла равен
б) косинус равен

2) (Ученик 5) Задача 2. Найдите
площадь треугольника, если

а) две стороны треугольника равны 20 см и 14 см, а
косинус угла между ними –
б) две стороны треугольника равны 17 см и 8 см, а
косинус угла между ними

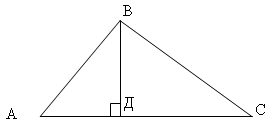
5. Обсуждение задачи 2б. Изменим
искомое в задаче 2б: Найдите квадрат третьей
стороны треугольника по алгоритму: (*)

1. Постройте высоту ВД.
2. Вычислите ВД.
3. Вычислите проекции сторон треугольника АВ
и ВС на АС (АД и ДС).
4. Из прямоугольного ДС вычислите ВС².

Запомните алгоритм и результат!

(Ответ. ВС² = 113)

Этап изучения нового материала. Слайд 4.
Теорема

В каждом треугольнике квадрат любой
стороны равен сумме квадратов двух других сторон
минус удвоенное произведение этих сторон на
косинус угла между ними.

Дано: АВС
АВ = с, АС = b, ВС = а
Доказать: c² = a² + b²
– 2 abcosC
Доказательство.
А) если о, тогда cosC = 0 и c² = a²
+ b² (Теорема Пифагора); Слайд 5.
Б) если – острый, то для доказательства
применим алгоритм (*):Слайд 6.

Пусть АД –
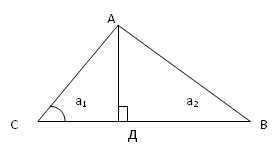
высота, АД = h. Из АДС а₁ = bcosC h²
= b² – a₁².
Из АДВ с²
= h² + (a – a₁)²,
с² = h² + a² – 2aa₁+
a₁²,
с² = b² – a₁² + a²
– 2abcosC + a₁² , т.е. c²
= a² + b² – 2abcosC.

В) если – тупой. Слайд 6.
Доказательство проведите самостоятельно.

Замечание: Вернитесь к измененной
домашней задаче 2б и вычислите ВД² по
теореме косинусов. Сравните ответы.

Работа с учебником

1. Прочитайте доказательство теоремы в учебнике
Л.С. Атанасяна Геометрия 7–9, стр.257.
2. Составьте алгоритм доказательства теоремы.
3. Расскажите основную идею доказательства.
4. Сравните доказательства. Найдите
положительные и отрицательные стороны обоих
доказательств.
5. Почему в доказательстве по учебнику не
рассматриваются три случая?

Основные задачи – следствия из теоремы
косинусов

1. Нахождение третьей стороны треугольника.
Слайд 7.

a = 11, b = 35, F C = 60;
a = 56, b = 9, F C = 120;
a = 31, b = 8, F C = 45.

2. СЛЕДСТВИЕ 1. Нахождение углов
треугольника. Слайд 8. Найдите
наибольший угол треугольника, если известны все
его стороны. Запишите соответствующие формулы
–следствия из теоремы косинусов

a = 8, b = 15, с = 13;
a = 80, b = 19, с = 91;
a = 11, с
= 7.

3. СЛЕДСТВИЕ 2.Определение вида
треугольника, зная его стороны (cлайд 9).

Задание: определите вид
треугольника с заданными сторонами, вычислив
предварительно косинус наибольшего угла:

23; 25; 34
7; 24; 25
6; 7; 9

Как можно ответить на этот вопрос без
вычисления косинуса наибольшего угла?

ВЫВОД.

Пусть с – наибольшая сторона
– если с² < a² + b²,
то треугольник остроугольный;
– если с² = a² + b²,
то треугольник прямоугольный;
– если с² > a² + b²,
то треугольник тупоугольный.

Проверьте вывод на выполненных задачах.

4. СЛЕДСТВИЕ 3. Формула медианы
треугольника. Слайд 10.

Дано: а, b, c
Найти: m_a

– Решение проведите самостоятельно.

Ответ. 4 m_a² = 2b²
+ 2c² – a²

Задача. Стороны треугольника 3; 4 и
6. Найти длину медианы, проведенной к большей
стороне.

5. СЛЕДСТВИЕ 4. В параллелограмме сумма
квадратов диагоналей равна сумме квадратов его
сторон: d₁² + d₂²
= 2a² + 2b² Слайд 11.

Доказательство проведите самостоятельно и
рассмотрите различные способы.

Задача. В параллелограмме
стороны равны 4 см и 6 см. Одна из диагоналей 8 см.
Найдите вторую диагональ.

– Дополняем теорию. (Задания на исследование по
группам) Какие ранее изученные теорем
можно доказать с помощью вывода теоремы
косинусов?

Ответ.

1. Теорема о средней линии треугольника. (Помогает
Слайд 12.)
2. Теорема о соотношении между сторонами и углами
треугольника. (Помогает Слайд 13)

Практическое приложение теоремы косинусов

По Слайдам 14, 15 составьте задачи о
нахождении расстояния между двумя недоступными
предметами и решите их.

Подведение итогов урока. Оцените
значимость изученного материала.

Домашенее задание: разобраться в
теории, найти другие способы решения
задач-следствий и оценить их; № 1025авд, 1030, 1031.

Источник

Технологическая
карта урока по геометрии 9 класса по теме:

«Теорема
косинусов»

Предмет: геометрия

Класс: 9

Тема: Теорема косинусов.

Тип урока: Урок изучения нового материала.

Цель: формирование ценностного отношения к пониманию и применению теоремы косинусов
в ходе коллективной, парной и самостоятельной учебно-познавательной
деятельности под руководством учителя.

Задачи урока:

Общебразовательная: повторить неравенство треугольника, теорему Пифагора, формулы
нахождения углов треугольников и их косинусов, площадей треугольников;
закрепить навыки использования теоремы косинусов для решения задач.

Развивающая: Обеспечение возможности каждому учащемуся достичь определенного
уровня; развитие умения самостоятельно добывать знания.

Воспитательная: Воспитание культуры общения, воспитание ответственности, воспитание
взаимопомощи.

Планируемые
результаты:

Ø
Личностные:
развитие самостоятельности мышлении учащихся в учебной деятельности.

Ø Предметные:
уметь применять теорему косинусов; формулировать решения задач с помощью
теоремы косинусов.

Ø Метапредметные:

·
познавательные – уметь использовать
математические знания для решения математических задач и оценки полученных
результатов; уметь работать с информацией, в том числе и с различными
математическими текстами.

·
регулятивные – уметь самостоятельно
обнаруживать и формулировать учебную проблему, определять цель; выдвигать
версии решения проблемы, осознавать конечный результат, выбирать средства
достижения цели и искать их самостоятельно; при необходимости исправлять ошибки
самостоятельно.

·
коммуникативные – умеют организовывать
учебное сотрудничество и совместную деятельность с учителем; участвуют в
диалоге.

Методы обучения: репродуктивный,
частично-поисковый.

Оборудование: Мультимедийный проектор, учебник
«Геометрия 7-9 класс» Л. С. Атанасян.

Структура урока:

1.
Организационный момент (2 мин).

2.
Актуализация опорных знаний (8 мин).

3.
Изучение нового материала (10 мин).

4.
Закрепление изученного материала (16 мин).

5.
Подведение итогов урока (3 мин).

6.
Домашнее задание (1 мин).

Этап урока	Задачи этапа	Деятельность учителя Содержание учебного материала	Деятельность учащихся	Формируемые УУД
1. Организационный момент	Создать благоприятный психологический настрой на работу, проверить готовность к уроку.	Учитель приветствует учащихся и проверяет готовность к уроку.	Приветствуют учителя, садятся на места.	Коммуникативные: слушают учителя. Регулятивные: самостоятельно организовывают свое рабочее место; настраиваются на продуктивную работу.
2. Актуализация опорных знаний	Устная фронтальная работа по вопросам теории данной темы, с целью актуализации знаний учащихся. Повторение изученного материала: теорема Пифагора, расстояние между двумя точками по их координатам, углы при параллельных прямых и их свойства, формулы приведения.	(Фронтальная работа с классом) 1. Как найти гипотенузу прямоугольного треугольника, если известны длины катетов a и b (Рис. 1.)? 2. Как найти катет a, если известны длина гипотенузы c и В? 3. Как найти катет b, если известны длина гипотенузы с и А? Рис. 1. 4. Чему равен квадрат расстояния между точками А (х1; у1) и В (х2; у2) (Рис. 2.)? 5. Найти координаты точки A, если OA = a и угол между положительной полуосью OX и лучом OA равен . Рис. 2. 6. a \| \| b. Что вы можете сказать об углах 1 и 2. Односторонние,1 +2 = 180⁰ . Если 2 = , тогда 1 = 180⁰— (Рис. 3.). 7. Чему равны: sin(180⁰— ) = ? и cos(180⁰— ) = ? Рис. 3.	Учащиеся по очереди отвечают на вопросы по рисункам. Проговаривают теорему Пифагора. Проговарнивают как найти расстояние между двумя точками по их координатам. Вспоминают про углы при параллельных прямых и их свойства и проговаривают их вслух. Вспоминают про формулы приведения и проговаривают их вслух.	Личностные: проявляют интерес к уроку. Коммуникативные: слушают учителя и вступают в диалог, выражают свои мысли. Регулятивные: отвечают на вопросы учителя.
3. Изучение нового материала	Формулировка темы и цели урока. Обеспечение закрепления в памяти учащихся знаний и способов действий, которые им понадобятся для самостоятельной работы с новым материалом.	Формулируется теорема косинусов через решение задачи. Учащимся предлагается задача на готовом чертеже. Теорема синусов для решения этой задачи не подходит, поскольку из трех известных элементов треугольника не известны сторона и противолежащий угол. Первый способ решения задачи. (Устно) Рис. 4. Дано: ABC, AC = b, AB = c, A. Найти: BC = a = ? Решение: Проведём CH – высоту. Прямоугольный ACH: AH = bcosA, CH = или CH = bsinA BH = AB – AH. CB²= a² = CH² + BH² a = . Второй способ решения задачи. Координатный метод. Рис. 5. I. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату. Решение записывают все учащиеся. II. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). Найдём квадрат стороны BC: a² = b² + c² – 2bccosA — теорема косинусов b² = a² + c² – 2accosB c² = b² + a² – 2abcosC Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними. По теореме косинусов можно найти любую сторону треугольника, зная длины двух других сторон и угол между ними. Теорему косинусов иногда называют обобщённой теоремой Пифагора. Почему? Объясните. Если С = 90⁰, то cosC = 0 и 2abcosC = 0, тогда c²= a² + b². Вывод: Теорема Пифагора является частным случаем теоремы косинусов. Рассмотрим следствия из теоремы косинусов 1 следствие. Рис. 6. Дано: ABC, AC = b, AB = c, AH = b_. Найти:a. Решение: Возможны 2 случая: а) A – острый, то cosA > 0, б) A – тупой, то cosA < 0, а) Если A – острый, тогда по теореме косинусов a² = b² + c² – 2bccosA. В прямоугольном ACH: b_c = bcosA. Так как A – острый, то cosA > 0, тогда a² = b² + c² – 2b_cc, то есть квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение одной из них на проекцию другой. б) Случай, когда угол, лежащий против неизвестной стороны тупой рассмотреть самостоятельно. Следующий урок начнём с проверки этого задания.(т.к. cosA < 0, то a² = b² + c² + 2bccosA, т.е. квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение одной из них на проекцию другой. 2 следствие. Рис. 7. Дано: ABCD – параллелограмм, AB = CD =a, BC = AD = b. Найти: d₁² + d₂² . Решение:ABC: d₁² = a² + b² – 2abcosB. ABD: d₂² = a² + b² – 2abcosA = a² + b² – 2abcos(180⁰ — B) = a² + b² + 2abcosB. d₁² + d₂² = a² + b² – 2abcosB + a² + b² + 2abcosB = a² + b² + a² + b². d₁² + d₂² = 2 a² + 2 b². Вывод: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. 3 следствие. Рис. 8. Дано: ABC, AB = c, AC = b, BC = a. Найти: . Решение: Достроим ABC до параллелограмма ABA₁C. AA₁² + BC² = 2b² + 2c² . BC = a, 2 = AA₁ . (2)² + a² = 2b² + 2c² 4² = 2(b² + c²) – a² ² = , = = , = Вывод: В любом треугольнике со сторонами a,b и c длины медиан m_a, , вычисляются по формулам: = , = , = .	Вступают в диалог с учителем. Решают вместе с учителем задачу. Записывают второй метод в тетрадь. Записывают решение. Записывают теорему в тетрадь. Отвечают на вопрос учителя. Записывают следствия в тетрадь. Решают вместе с учителем задачу.	Познавательные: извлекают необходимую информацию из текста; структурируют учебный материал, выделяя в нем главное, ориентируются в своей системе знаний: отличают новое от уже известного. Коммуникативные: слушают и понимают речь учителя.
4. Закрепление изученного материала	Умение самостоятельно выполнять задания и решать задачи.	Задача: В треугольнике две стороны равны 20 см и 21 см, а синус угла между ними равен 0,6 . Найти третью сторону. Сколько решений имеет задача? Рис. 9. Дано: sin = 0,6, AB = 20 см, AC = 21 см. Найти: BC. Решение: sin = 0,6 может быть острым или тупым. 1 случай: — острый BC² = AB² + AC² – 2ABACcos. Так как — острый, то cos>0. Тогда cos = = = = 0.8 BC = = = 13(см). 2 случай: — тупой. Рис. 10. BC² = AB² + AC² – 2ABACcos Так как — тупой, то cos<0, cos = —= — = -0.8 BC = = (см). Ответ: 1) BC = 13 см. 2) BC = см.	Решают в тетрадях и у доски упражнения вместе с учителем.	Познавательные: используют новую информацию для выполнения учебных заданий. Коммуникативные: строят речевые высказывания в соответствии с поставленными задачами; оформляют свои мысли в письменной форме.
5. Подведение итогов урока	Оценка своей деятельности и деятельности других учащихся.	Учитель подводит итоги урока. Спрашивает: Что нового вы сегодня узнали? Просит закончить фразу: -я узнал -еще хочу узнать -чему научились? -где пригодятся новые знания? Далее учитель озвучивает, кто хорошо работал на уроке, и выставляет оценки.	Учащиеся слушают и отвечают на вопросы учителя. Совместно с учителем оценивают свою работу на уроке.	Познавательные: обобщают изученное. Коммуникативные: оформляют свои мысли в устной форме, отвечают на вопросы учителя. Регулятивные: анализируют и осмысливают свои достижения; совместно с учителем и одноклассниками дают оценку деятельности на уроке.
6. Домашнее задание	Обеспечить понимание учащимися материала	п. 98 №1025(б, в, г).	Записывают домашнее задание в дневники.

Источник

Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов:

asinA=bsinB=csinC

(в решении задачи одновременно пишутся две части, они образуют пропорцию).

Теорема синусов используется для вычисления:

неизвестных сторон треугольника, если даны два угла и одна сторона;
неизвестных углов треугольника, если даны две стороны и один прилежащий угол.

Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения

sin180°−α=sinα

Наиболее часто используемые тупые углы:

sin120°=sin180°−60°=sin60°=32;sin150°=sin180°−30°=sin30°=12;sin135°=sin180°−45°=sin45°=22.

Радиус описанной окружности

asinA=bsinB=csinC=2R

, где (R) — радиус описанной окружности.

Выразив радиус, получаем

R=a2sinA

, или

R=b2sinB

, или

R=c2sinC

Для вычисления элементов прямоугольного треугольника достаточно (2) данных величин (две стороны или сторона и угол).

Для вычисления элементов произвольного треугольника необходимо хотя бы (3) данных величины.

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Также теорема исполняется для любой стороны треугольника:

Теорема косинусов используется для вычисления:

неизвестной стороны треугольника, если даны две стороны и угол между ними;
вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.

Значение косинуса тупого угла находится по формуле приведения

cos180°−α=−cosα

Наиболее часто используемые тупые углы:

cos120°=cos180°−60°=−cos60°=−12;cos150°=cos180°−30°=−cos30°=−32;cos135°=cos180°−45°=−cos45°=−22.

Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.

Источники:

Рис. 1-3. Треугольник, окружность, © ЯКласс.

Источник

Прежде чем
приступить к изучению нового материала, давайте, вспомним: формулы для
вычисления площади треугольника и параллелограмма.

Формулы для
вычисления площади треугольника:

Формулы для вычисления площади параллелограмма:

Теорема синусов:

Стороны
треугольника пропорциональны синусам противолежащих углов.

Расширенная
теорема синусов:

Расстояние между
двумя точками:

Сегодня на уроке мы
с вами сформулируем и докажем теорему косинусов.

Теорема. Квадрат
стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
произведение этих сторон, умноженное на косинус

угла между ними.

Докажем это.

Что и
требовалось доказать.

Частным случаем
теоремы косинусов является теорема Пифагора.

Давайте рассмотрим
прямоугольный треугольник и запишем для него теорему косинусов.

Именно поэтому
теорему косинусов называют обобщенной теоремой Пифагора.

Задача. Найти
сторону треугольника , если:

а) , ; б) , ;

в) , .

Решение.

Запишем теорему
косинуса для стороны AB.

а)

б)

в)

Задача. Найти
косинус наибольшего угла треугольника , если стороны этого
треугольника равны: а) , , ; б) , , ;

в) , , .

Решение.

а)

−
треугольник остроугольный

б)

−
треугольник тупоугольный

в)

− треугольник
прямоугольный

Давайте подробнее
рассмотрим выражения для косинуса угла.

В знаменателе дроби
всегда находится положительное число, потому что стороны треугольника могут
иметь только положительные длины. Значит, знак косинуса зависит от числителя. В
числителе у нас находится разность.

Пусть наибольшая сторона
треугольника, тогда если:

ü
, то треугольник
остроугольный

ü
, то треугольник
прямоугольный

ü
, то треугольник
тупоугольный

Задача.
Определить вид треугольника со сторонами:

а) 23, 25, 34; б)
7, 24, 25; в) 6, 7, 9.

Решение.

Эту задачу мы будем
решать двумя способами: с помощью только что сформулированных утверждений и
вычислив косинус наибольшего угла.

а) Решая первым
способом, мы получим, что в первом случае у нас тупоугольный треугольник. ,

треугольник
тупоугольный.

Давайте проверим
это.

Косинус
отрицательный, значит, наибольший угол треугольника – тупой, то есть
треугольник тупоугольный.

б) ,

треугольник
прямоугольный

в) ,

треугольник
остроугольный

Решая эту задачу,
мы убедились в том, что утверждения действительно справедливы для любого
треугольника. Эти утверждения называют следствием из теоремы косинусов.

Пусть наибольшая сторона
треугольника, тогда если:

ü
, то треугольник
остроугольный

ü
, то треугольник
прямоугольный

ü
, то треугольник
тупоугольный

Задача. Доказать,
что для произвольного треугольника справедлива формула:

Доказательство.

Это формула называется
формулой медиан треугольника.

Задача. В
треугольнике найти длины всех
медиан, если , , .

Решение.
Воспользуемся только что доказанной формулой. Очевидно, что будут выполняться
аналогичные формулы для медиан к сторонам b и c. Тогда несложно вычислить длины всех медиан треугольника…

Задача. Доказать,
что для любого параллелограмма .

Решение.

Задача. Стороны
параллелограмма равны и . Одна из диагоналей
равна . Найти вторую
диагональ.

Решение.

Воспользуемся
только что доказанным утверждением.

Задача. Две
стороны треугольника равны и , . Найти третью сторону
треугольника.

Решение.

Для нахождения
неизвестной стороны, воспользуемся теоремой косинуса.

Запишем основное
тригонометрическое тождество и найдем, что

или

Подведем итоги
урока. Сегодня на уроке мы сформулировали и доказали теорему косинусов. Вывели
следствие их этой теоремы. Познакомились с формулой для нахождения длины
медианы треугольников, а также познакомились с формулой связывающей диагонали и
стороны параллелограмма.

Источник

Стандартные обозначения углов и сторон треугольника

Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора на произвольные плоские треугольники.

Формулировка[править | править код]

Для плоского треугольника со сторонами a,b,c и углом alpha , противолежащим стороне ,
справедливо соотношение:

${displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha .}$

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними^[1]

Доказательства[править | править код]

Классическое доказательство

Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:

откуда

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

$h^{2}=b^{2}-(bcos alpha )^{2}qquad qquad qquad (1)$

$h^{2}=a^{2}-(c-bcos alpha )^{2}qquad qquad (2)$

Приравниваем правые части уравнений (1) и (2) и:

$b^{2}-(bcos alpha )^{2}=a^{2}-(c-bcos alpha )^{2}$

или

$a^{2}=b^{2}+c^{2}-2bccos alpha$

Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.

Выражения для сторон b и c:

$b^{2}=a^{2}+c^{2}-2accos beta$

$c^{2}=a^{2}+b^{2}-2abcos gamma$

Доказательство через координаты

Одним из доказательств является доказательство её в координатной плоскости.

Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c, AC=b, CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα).
Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:
$a^{2}=(bcos {a}-c)^{2}+b^{2}sin ^{2}{a}$
$a^{2}=b^{2}cos ^{2}{a}-2bccos {a}+c^{2}+b^{2}sin ^{2}{a}$
$a^{2}=b^{2}(cos ^{2}{a}+sin ^{2}{a})+c^{2}-2bccos {a}$
Так как
$cos ^{2}{a}+sin ^{2}{a}=1$ (основное тригонометрическое тождество), то
$a^{2}=b^{2}+c^{2}-2bccos {a}$
Теорема доказана.
Для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² — известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.

Доказательство через векторы

Ниже подразумеваются операции над векторами, а не длинами отрезков
${displaystyle AC=AB+BC=>BC=AC-AB=>BC^{2}=AC^{2}+AB^{2}-2cdot ACcdot AB}$

Так как скалярное произведение векторов равно произведению их модулей (длин) на косинус угла между ними, последнее выражение можно переписать:
${displaystyle a^{2}=b^{2}+c^{2}-2cdot bcdot ccdot cos alpha }$
где a, b, c — длины соответствующих векторов

Следствия[править | править код]

Теорема косинусов может быть использована для нахождения косинуса угла треугольника

$cos {alpha }={frac {b^{2}+c^{2}-a^{2}}{2bc}}$

В частности,

Теорема косинусов может быть записана также в следующем виде^[2]:

$a^{2}=(b+c)^{2}-4cdot bcdot ccdot cos ^{2}(alpha /2)$

$a^{2}=(b-c)^{2}+4cdot bcdot ccdot sin ^{2}(alpha /2)$

Доказательство

Последние две формулы мгновенно следуют из основной формулы теоремы косинусов (см. в рамке выше), если в правой её части воспользоваться формулами разложения квадрата суммы (для второй формулы — квадрата разности) двух членов на квадратный трехчлен, являющийся полным квадратом. Для получения окончательного результата (двух формул выше) в правой части надо еще воспользоваться известными тригонометрическими формулами:

$1+cos alpha =2cdot cos ^{2}(alpha /2)$

$1-cos alpha =2cdot sin ^{2}(alpha /2)$

Кстати, вторая формула формально не содержит косинусов, но её все равно именуют теоремой косинусов.

Для других углов[править | править код]

Теорема косинусов для двух других углов имеет вид:

${displaystyle c^{2} =a^{2}+b^{2}-2abcos gamma }$

${displaystyle b^{2} =a^{2}+c^{2}-2accos beta }$

Из этих и из основной формулы могут быть выражены углы:

${displaystyle alpha =arccos left({frac {b^{2}+c^{2}-a^{2}}{2bc}}right)}$

${displaystyle beta =arccos left({frac {a^{2}+c^{2}-b^{2}}{2ac}}right)}$

${displaystyle gamma =arccos left({frac {a^{2}+b^{2}-c^{2}}{2ab}}right)}$

История[править | править код]

Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.

Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях ал-Баттани.^[3]^:105
Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» по имени ал-Баттани.

В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии.
В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.

Вариации и обобщения[править | править код]

Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трёхгранного угла.
Теоремы косинусов (геометрия Лобачевского)
Тождество параллелограмма. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон (см. также Теорема Птолемея):

$AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}.$

Для евклидовых нормированных пространств[править | править код]

Пусть в евклидовом пространстве задана норма, ассоциированная со скалярным произведением, то есть . Тогда теорема косинусов формулируется следующим образом:

Теорема.
$leftVert {vec {a}}-{vec {b}}rightVert ^{2}=leftVert {vec {a}}rightVert ^{2}+leftVert {vec {b}}rightVert ^{2}-2({vec {a}},{vec {b}})$

Для четырёхугольников[править | править код]

Возводя в квадрат тождество можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников:

$d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B-2accos omega -2bccos angle C$

, где

— угол между прямыми AB и CD.

Или иначе:

$d^{2}=a^{2}+b^{2}+c^{2}-2abcos angle B+2accos(angle A+angle D)-2bccos angle C$

Формула справедлива и для тетраэдра, под

подразумевается угол между скрещивающимися ребрами.

С помощью неё можно найти косинус угла между скрещивающимися ребрами

зная все ребра тетраэдра:

${displaystyle cos w=(b^{2}+d^{2}-e^{2}-f^{2})/2ac}$

Где

пары скрещивающихся ребер тетраэдра.

Косвенный аналог для четырёхугольника[править | править код]

Соотношение Бретшнайдера — соотношение в четырёхугольнике, косвенный аналог теоремы косинусов:

Между сторонами a, b, c, d и противоположными углами и диагоналями e, f простого (несамопересекающегося) четырёхугольника выполняется соотношение:

${displaystyle e^{2}f^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcdcos(alpha +gamma )}$

Если четырёхугольник вырождается в треугольник, и одна вершина попадает на сторону, то получается теорема Стюарта.
Теорема косинусов для треугольника является частным случаем соотношения Бретшнайдера, если в качестве четвёртой вершины выбрать центр описанной окружности треугольника.

Симплексы[править | править код]

${displaystyle S_{i}S_{j}cos angle A={frac {(-1)^{(n-1+i+j)}}{2^{n-1}((n-1)!)^{2}}}{begin{vmatrix}0&1&1&1&dots &1\1&0&d_{12}^{2}&d_{13}^{2}&dots &d_{1(n+1)}^{2}\1&d_{21}^{2}&0&d_{23}^{2}&dots &d_{2(n+1)}^{2}\1&d_{31}^{2}&d_{32}^{2}&0&dots &d_{3(n+1)}^{2}\vdots &vdots &vdots &vdots &ddots &vdots \1&d_{(n+1)1}^{2}&d_{(n+1)2}^{2}&d_{(n+1)3}^{2}&dots &0\end{vmatrix}}}$

при этом мы должны зачеркнуть строку и столбец, где находится $d_{ij}$ или $d_{ji}$ .

A — угол между гранями $S_{i}$ и $S_{j}$ , $S_{i}$ -грань, находящаяся против вершины i, $d_{ij}$ — расстояние между вершинами i и j.

См. также[править | править код]

Решение треугольников
Скалярное произведение
Соотношение Бретшнайдера
Теорема косинусов для трёхгранного угла
Теорема о проекциях
Теорема Пифагора
Сферическая теорема косинусов
Теорема котангенсов
Теорема синусов
Теорема тангенсов
Тригонометрические тождества
Тригонометрические функции

Примечания[править | править код]

↑ Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 7—9: учеб. для общеобразоват. учреждений — 15-е изд. — М.: Просвещение, 2005. — С. 257. — 384 с.: ил. — ISBN 5-09-014398-6
↑ ¹ ² Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — С. 51. — 832 с.
↑ Florian Cajori. A History of Mathematics — 5th edition 1991

Литература[править | править код]

Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 84—85. — ISBN 5-94057-170-0.

Источник

Формулировка[править | править код]

Доказательства[править | править код]

Следствия[править | править код]

Для других углов[править | править код]

История[править | править код]

Вариации и обобщения[править | править код]

Для евклидовых нормированных пространств[править | править код]

Для четырёхугольников[править | править код]

Косвенный аналог для четырёхугольника[править | править код]

Симплексы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Добавить комментарий Отменить ответ