Теорема грина для многосвязной области - Универсальный справочник

Формула Грина

Связность, односвязность, многосвязность

Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.

Множество точек { на прямой, на плоскости, в пространстве } называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Область { на плоскости, в пространстве } называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.

Примеры:

Односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.

Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.

Теорема Грина для односвязной области

Пусть на плоскости $mathbf { textit { Oxy } } $ задана односвязная область$mathbf { textit { D } } $, ограниченная кусочно-гладким контуром $mathbf { textit { C } } $. На множестве $bar { D } =Dcup C$ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные.

Тогда $ointlimits_С { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $, при этом контур$mathbf { textit { C } } $ обходится так, что область $mathbf { textit { D } } $ остаётся слева.

Доказательство

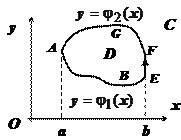
1). Пусть $mathbf { textit { D } } $ — простая область. Докажем сначала, что $ointlimits_C { P(x,y)dy } =-iintlimits_D { frac { partial P } { partial y } dxdy } $.

$y=varphi _2 (x)y=varphi _1 (x)$

Опишем $mathbf{textit{D}}$ неравенствами $D:left({begin{array}{l} aleqslant xleqslant b, \ varphi _1 (x)leqslant yleqslant varphi _2 (x). \ end{array}}right.$

Тогда $-iintlimits_D { frac { partial P } { partial y } dxdy } =-intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _x (x) } { frac { partial P } { partial y } dy } } =-intlimits_a^b { left. { P(x,y) }right|_ { varphi _1 (x) } ^ { varphi _2 (x) } dx } =-intlimits_a^b { P(x,varphi _2 (x))dx } — +intlimits_a^b { P(x,varphi _1 (x))dx } = \ =intlimits_a^b { P(x,varphi _1 (x))dx } -intlimits_b^a { P(x,varphi _2 (x))dx } =intlimits_ { mathop { ABE } limits^cup } { P(x,y)dx } + intlimits_ { mathop { FGA } limits^cup } { P(x,y)dx } $.

Если контур включает вертикальные участки, такие как $mathbf { textit { EF } } $, то на этих участках $mathbf { textit { dx } } = 0$, поэтому $intlimits_ { mathop { EF } limits^cup } { P(x,y)dx } =0$, и $y=psi _2 (y)y=psi _1 (y)-iintlimits_D { frac { partial P } { partial y } dxdy } =intlimits_ { mathop { ABE } limits^cup } { P(x,y)dx } +intlimits_ { mathop { EF } limits^cup } { P(x,y)dx } +intlimits_ { mathop { FGA } limits^cup } { P(x,y)dx } =ointlimits_C { P(x,y)dx } $, что и требовалось доказать.

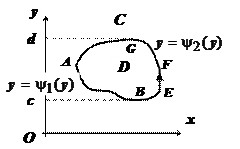
Равенство $ointlimits_C { Q(x,y)dy } =iintlimits_D { frac { partial Q } { partial x } dxdy } $ доказывается точно также:

$iintlimits_D { frac { partial Q } { partial x } dxdy } =intlimits_c^d { dyintlimits_ { psi _1 (y) } ^ { psi _2 (y) } { frac { partial Q } { partial x } dx } } =intlimits_c^d { left. { Q(x,y) }right|_ { psi _1 (y) } ^ { psi _2 (y) } dy } = intlimits_c^d { Q(psi _2 (y),y)dy } -intlimits_c^d { Q(psi _1 (y),y)dy } = \ = intlimits_ { mathop { BEFG } limits^cup } { Q(x,y)dy } + intlimits_ { mathop { GAC } limits^cup } { Q(x,y)dy } =ointlimits_C { Q(x,y)dy } $.

Суммируя равенства $ointlimits_C { P(x,y)dy } =-iintlimits_D { frac { partial P } { partial y } dxdy } $ и $ointlimits_C { Q(x,y)dy } =iintlimits_D { frac { partial Q } { partial x } dxdy } $, получим одну из важнейших формул анализа — формулу Грина $ ointlimits_С { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $

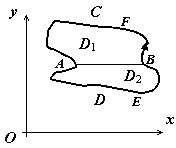
2). Пусть теперь $mathbf { textit { D } } $ — произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком $mathbf { textit { АВ } } $ и пусть подобласти $mathbf { textit { D } } _ { 1 } $ и $mathbf { textit { D } } _ { 2 } $ — результат разбиения. Для этих подобластей формула Грина доказана:

$ointlimits_ { ABFA } { Pdx+Qdy=iintlimits_ { D_1 } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $ и $ointlimits_ { AEBA } { Pdx+Qdy=iintlimits_ { D_2 } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $.

По свойству аддитивности $ointlimits_ { ABFA } { Pdx+Qdy } =ointlimits_ { AB } { Pdx+Qdy } +ointlimits_ { BFA } { Pdx+Qdy } $, $ointlimits_ { AEBA } { Pdx+Qdy } =ointlimits_ { AEB } { Pdx+Qdy } +ointlimits_ { BA } { Pdx+Qdy } = ointlimits_ { AEB } { Pdx+Qdy } -ointlimits_ { AB } { Pdx+Qdy } $

Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам $mathbf { textit { АВ } } $ и $mathbf { textit { ВА } } $ взаимно уничтожаются, а сумма интегралов по кривым $mathbf { textit { BFA } } $ и $mathbf { textit { AEB } } $ даёт интеграл по контуру $mathbf { textit { C } } $, т.е. формула Грина верна и для области, не являющейся простой.

Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.

Теорема Грина для многосвязной области

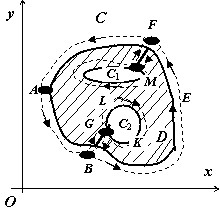
Пусть теперь $mathbf { textit { D } } $ многосвязная на плоскости $mathbf { textit { Oxy } } $. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек.

Рассмотрим случай, когда граница области $mathbf { textit { D } } $ { на рисунке область заштрихована } состоит из внешнего контура $mathbf { textit { C } } $ и внутренних контуров $mathbf { textit { C } } _ { 1 } $ и $mathbf { textit { C } } _ { 2 } $.

Соединим контур $mathbf { textit { C } } $разрезом $mathbf { textit { FM } } $ с контуром $mathbf { textit { C } } _ { 1 } $, разрезом $mathbf { textit { BG } } $ — с контуром $mathbf { textit { C } } _ { 2 } $. { Под словами «соединим разрезом $mathbf { textit { BG } } $ » подразумевается то, что мы удалим из $mathbf { textit { D } } $ отрезок $mathbf { textit { BG } } )$.

Область $ { D } ‘=Dbackslash (BGcup FM)$ с границей $ { Gamma } ‘=mathop { AB } limits^cup cup BGcup (C_2 =mathop { GLKG } limits^cup )cup GBcup mathop { BF } limits^cup cup FMcup C_1 cup MFcup mathop { MA } limits^cup $ односвязна, поэтому для неё справедлива формула Грина:

$ointlimits_ { { Gamma } ‘ } { Pdx+Qdy=iintlimits_ { { D } ‘ } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $

Двойные интегралы по областям $mathbf { textit { D } } $ и $ { D } ‘mathbf { } $ равны { площадь разрезов равна нулю } ; в криволинейный интеграл по кусочно-гладкой кривой $ { Gamma } ‘$ интегралы по разрезам входят с противоположными знаками { $intlimits_ { BG } { Pdx } +Qdy$ и $intlimits_ { GB } { Pdx } +Qdy$, например } и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области :

пусть на плоскости $mathbf { textit { Oxy } } $ дана многосвязная область$mathbf { textit { D } } $ с границей $Gamma $. На множестве $bar { D } =Dcup Gamma $ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные. Тогда $ointlimits_Gamma { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $, при этом каждая часть полной границы $Gamma $ обходится так, что область $mathbf { textit { D } } $ остаётся слева.

Источник

Формула Грина на плоскости

разделов

от теории до практики

примеров

Примеры решения задач

видео

Примеры решения задач

Ориентация границы плоской области.

Начать изучение
Формула Грина.

Начать изучение
Формула Грина для многосвязной области.

Начать изучение
Применение формулы Грина к вычислению площадей.

Начать изучение
Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).

Начать изучение

Ориентация границы плоской области.

Напомним, что областью в (boldsymbol{R}^{2}) называется открытое связное множество, а замыкание области получается присоединением к области ее границы.

Теорема Жордана утверждает, что любая простая (без точек самопересечения) замкнутая кривая разделяет плоскость на две области, ограниченную и неограниченную, общей границей которых она является.

Рис. 51.1

Область (Omega subset boldsymbol{R}^{2}) называется односвязной, если для любого простого контура (gamma subset Omega) ограничиваемая этим контуром область (Omega_{1} subset Omega). В частности, область на рис. 51.1 односвязна.

Будем говорить, что простой контур (Gamma) ориентирован положительно, если при обходе контура ограничиваемая им область остается слева (рис. 51.1). Противоположно ориентированный контур будем обозначать через (Gamma^{-}).

Формула Грина.

Теорема.

Пусть функции (P(x, y)) и (Q(x, y)) непрерывно дифференцируемы в односвязной области (Omega subset boldsymbol{R}^{2}), а простой кусочно гладкий контур (Gamma subset Omega) ограничивает область (G subset Omega). Тогда справедлива формула Грина
$$
intlimits_{partial G} P dx + Q dy = iintlimits_{G} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy,label{ref1}
$$
где (partial G) есть положительно ориентированная граница области (G).

Доказательство.

(circ) Докажем сначала формулу eqref{ref1} в наиболее простом случае, когда область (G) еще и элементарна относительно обеих координатных осей, то есть существуют такие кусочно непрерывно дифференцируемые и непрерывные функции (varphi(x)), (psi(x)), (x in [a, b]), и (alpha(y)), (beta(y)), (y in [c, d]), что (рис. 51.2)
$$
overline{G} = {(x, y): a leq x leq b, varphi(x) leq y leq psi(x)} = {(x, y): c leq y leq d, alpha(x) leq x leq beta(x)}.nonumber
$$

Рис. 51.2

Примерами таких областей являются внутренности круга, эллипса, треугольника.

Применяя формулу сведения двойного интеграла к повторному, получаем равенства
$$
iintlimits_{G} frac{partial P}{partial y} (x, y) dx dy =-intlimits_{a}^{b} dx intlimits_{varphi(x)}^{psi(x)} frac{partial P}{partial y} (x, y) dx dy =\= intlimits_{a}^{b} P(x, varphi(x))dx-intlimits_{a}^{b} P(x, psi(x))dx =\= intlimits_{ABCD} P dx + intlimits_{DE} P dx + intlimits_{EFMN} P dx + intlimits_{NA} P dx = intlimits_{partial G} P dx.label{ref2}
$$

При выводе формулы eqref{ref2} была использована формула для криволинейного интеграла (intlimits_{Gamma} P dx) по кривой (Gamma), являющейся графиком функции. Добавленные интегралы по вертикальным отрезкам (DE) и (NA) равны нулю, так как на этих отрезках (x = operatorname{const}).

Аналогично доказывается формула
$$
iintlimits_{G} frac{partial Q(x, y)}{partial x} dx dy = intlimits_{partial G} Q(x, y) dy.label{ref3}
$$

Складывая равенства eqref{ref2} и eqref{ref3}, получаем формулу Грина eqref{ref1}.

Пусть теперь область (G) по-прежнему ограничена кусочно гладкой замкнутой кривой (partial G). Предположим, что ее можно кусочно гладкой простой кривой (Gamma) (перегородкой) разбить на две области простейшего вида, рассмотренные выше (рис. 51.3). Тогда
$$
partial G_{1} = Gamma cup Gamma_{1}, partial G_{2} = Gamma^{-} cup Gamma_{2}.nonumber
$$

Рис. 51.3

Применяя формулу Грина в каждой из областей (G_{1}) и (G_{2}), получаем
$$
iintlimits_{G_{1}} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy = intlimits_{partial G} P dx + Q dy = intlimits_{Gamma_{1}} P dx + Q dy + intlimits_{Gamma} P dx + Q dy,nonumber
$$
$$
iintlimits_{G_{1}} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy = intlimits_{Gamma_{2}} P dx + Q dy + intlimits_{Gamma^{-}} P dx + Q dy.nonumber
$$

Складывая эти два равенства и учитывая, что криволинейные интегралы по противоположно ориентированным кривым (Gamma) и (Gamma^{-}) взаимно уничтожаются, получаем, что формула Грина eqref{ref1} верна для области (G = G_{1} cup G_{2}).

При помощи математической индукции теперь легко обобщить формулу Грина на односвязную область, которая при помощи (n-1) непересекающихся гладких перегородок разбивается на области (G_{1}, ldots, G_{n}) простейшего вида (рис. 51.3). В частности, формула Грина обобщается на многоугольные области, ограниченные простыми замкнутыми ломаными. В общем случае можно доказать формулу Грина, аппроксимируя область с кусочно гладкой границей многоугольной областью. (bullet)

Формула Грина для многосвязной области.

Формула Грина может быть обобщена и на случай многосвязной ((n)-связной) области, ограниченной внешним контуром (Gamma) и непересекающимися внутренними контурами (gamma_{1}, ldots, gamma_{n-1}). Все контуры предполагаются кусочно гладкими. На рис. 51.4 изображены ограниченные двусвязная и трехсвязная области.

Рис. 51.4

Внешний контур ориентируем так, чтобы при его обходе область оставалась слева. Так ориентированный контур будем обозначать (Gamma). А внутренние контуры ориентируем так, чтобы при их обходе область (G) оставалась справа. Будем писать
$$
partial G = left(bigcup_{i=1}^{n} gamma_{i}^{-}right) bigcup Gamma.nonumber
$$

Пусть непрерывно дифференцируемое поле ((P(x, y), Q(x, y))) задано в двусвязной области (G), ограниченной кусочно гладкими простыми контурами: внешним (Gamma) и внутренним (gamma) (рис. 51.4).

При помощи гладких перегородок (gamma_{3}) и (gamma_{4}) (рис. 51.5) разделим двусвязную область (G) на две односвязных, (G_{1}) и (G_{2}). Как видно из рис. 51.5,
$$
Gamma = Gamma_{1} cup Gamma_{2}, gamma = gamma_{1} cup gamma_{2}.nonumber
$$

Рис. 51.5

Применяя к (G_{1}) и (G_{2}) формулу Грина для односвязной области, получаем (рис. 51.5)
$$
iintlimits_{G_{1}} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G_{1}} P dx + Q dy = left(intlimits_{Gamma_{1}} + intlimits_{gamma_{3}} + intlimits_{gamma_{1}^{-}} + intlimits_{gamma_{4}}right) (P dx + Q dy),nonumber
$$
$$
iintlimits_{G_{2}} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G_{1}} P dx + Q dy = left(intlimits_{Gamma_{2}} + intlimits_{gamma_{4}^{-}} + intlimits_{gamma_{2}^{-}} + intlimits_{gamma_{3}^{-}}right) (P dx + Q dy),nonumber
$$
где в правой части употреблено сокращенное обозначение для суммы четырех криволинейных интегралов по соответствующим кривым. Складывая эти равенства и учитывая, что криволинейные интегралы по противоположно ориентированным кривым взаимно уничтожаются, получаем
$$
iintlimits_{G} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{Gamma} P dx + Q dy + intlimits_{gamma^{-}} P dx + Q dy = intlimits_{partial G} P dx + Q dy.nonumber
$$

Формально формула Грина для двусвязной области имеет тот же вид, что и для односвязной, если (displaystyleintlimits_{partial G} P dx + Q dy) понимать как сумму криволинейных интегралов по (Gamma) и (gamma^{-}).

Индукцией эта формула Грина обобщается и на (n)-связную область:
$$
iintlimits_{G} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G} P dx + Q dy = intlimits_{Gamma} P dx + Q dy + sum_{i=1}^{substack{n-1}} intlimits_{gamma_{i}^{-}} P dx + Q dy.nonumber
$$

Применение формулы Грина к вычислению площадей.

Полагая в формуле Грина eqref{ref1} (Q = x), (P = -y), получаем формулу для вычисления площади, ограниченной гладким контуром,
$$
m(G) = frac{1}{2} intlimits_{partial G} x dy-y dx.label{ref4}
$$

Иногда при практическом применении формулы eqref{ref4} полезно воспользоваться тем, что
$$
x dy-y dx = (x^{2} + y^{2})dleft(operatorname{arctg} frac{y}{x}right).nonumber
$$

Пример 1.

Найти площадь, ограниченную кривой (рис. 51.6)
$$
x = frac{3at}{1 + t^{3}},quad y = frac{3at^{2}}{1 + t^{3}},quad 0 leq t leq +infty.nonumber
$$

Рис. 51.6

Решение.

(vartriangle) Эта кривая (декартов лист), как нетрудно показать, симметрична относительно прямой (y = x).

Поэтому можно ограничиться вычислением площади половинки листа, для которой (0 leq t leq 1). Получаем
$$
x dy-y dx = (x^{2} + y^{2})dleft(operatorname{arctg} frac{y}{x}right) = frac{9a^{2}t^{2}(1 + t^{2})}{(1 + t^{3})^{2}}d(operatorname{arctg} t) = frac{9a^{2}t^{2}}{(1 + t^{3})^{2}}dt = -3a^{2} dleft(frac{1}{1 + t^{3}}right).nonumber
$$

По формуле eqref{ref4} площадь половинки листа Декарта равна
$$
m(G) = frac{1}{2} intlimits_{Gamma} x dy-y dx = -frac{3a^{2}}{2} intlimits_{0}^{1} dleft(frac{1}{1 + t^{3}}right) = frac{3a^{2}}{4},nonumber
$$
а искомая площадь равна (displaystylefrac{3a^{2}}{2}). (blacktriangle)

Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).

Пусть в области (G subset boldsymbol{R}^{2}) задано непрерывное векторное поле ((P(x, y), Q(x, y))). Например, это может быть силовое поле. Возьмем в области (G) две произвольные точки, (A(x_{0}, y_{0})) и (B(x, y)). Соединим эти две точки кусочно гладкой кривой (Gamma_{AB}), лежащей в (G). Вычислим интеграл (displaystyleintlimits_{Gamma_{AB}} P dx + Q dy). Этот интеграл можно интерпретировать как работу силы при движении точки по кривой (Gamma_{AB}). Вообще говоря, (displaystyleintlimits_{Gamma_{AB}} P dx + Q dy) зависит как от точек (A) и (B), так и от пути, по которому мы из точки (A) приходим в точку (B). Наша цель — выяснить условия независимости величины этого интеграла (работы силы) от пути интегрирования.

Теорема 1.

Следующие три условия эквивалентны:

для любой замкнутой ломаной (L subset G)
$$
intlimits_{L} P dx + Q dy = 0;label{ref5}
$$
(displaystyleintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB} subset G), соединяющей точки (A) и (B);
поле ((P(x, y), Q(x, y))) потенциально, то есть существует такая непрерывно дифференцируемая функция (U(x, y)) (потенциал поля), что
$$
P(x, y) dx + Q(x, y) dy = dU,nonumber
$$
$$
P(x, y) = frac{partial U(x, y)}{partial x},quad Q(x, y) = frac{partial U(x, y)}{partial y}.nonumber
$$

Доказательство.

(circ) Доказательство проведем по круговой схеме: (1.Rightarrow 2. Rightarrow 3.Rightarrow 1.)

Докажем, что (1. Rightarrow 2.) Пусть выполнено условие (1.) Возьмем две произвольных точки, (A) и (B), в области (G). Соединим их ломаной (L_{AB}). Пусть (L’_{AB}) — любая другая ломаная, соединяющая точки (A) и (B). Тогда (L = L_{AB} + L’_{BA}) есть замкнутая ломаная. В силу условия (1.) имеем
$$
0 = intlimits_{L} P dx + Q dy = intlimits_{L_{AB}} P dx + Q dy + intlimits_{L’_{BA}} P dx + Q dy =\= intlimits_{L_{AB}} P dx + Q dy-intlimits_{L’_{BA}} P dx + Q dy,nonumber
$$
$$
intlimits_{L_{AB}} P dx + Q dy = intlimits_{L’_{BA}} P dx + Q dy,nonumber
$$
то есть интеграл (nonumberintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB}), соединяющей точки (A) и (B).
Докажем, что (2. Rightarrow 3.) Пусть (displaystyleintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB}), соединяющей точки (A) и (B). Фиксируем точку (A(x_{0}, y_{0})), а точку (B(x, y)) будем считать переменной. Тогда (displaystyleintlimits_{L_{AB}} P dx + Q dy) зависит только от точки (B), и, следовательно, в области (G) определена функция
$$
U(x, y) = intlimits_{L_{AB}} P dx + Q dy.nonumber
$$
Покажем, что функция (U(x, y)) — потенциал поля. Соединим точки (B(x, y)) и (C(x + Delta x, y)) отрезком (BC), лежащим в области (G) (рис. 51.7). Это всегда можно сделать при достаточно малом (Delta x), так как (G) — открытое множество. Тогда
$$
frac{1}{Delta x} (u(x + Delta x, y)-U(x, y)) = frac{1}{Delta x} left[intlimits_{L_{ABC}} P dx + Q dy-intlimits_{L_{AB}} P dx + Q dyright] =\= frac{1}{Delta x} intlimits_{BC} P dx + Q dy = frac{1}{Delta x} intlimits_{x}^{x + Delta x} P(xi, y) dxi.nonumber
$$

Рис. 51.7
Применяя при фиксированном (y) к непрерывной функции (P(xi, y)) интегральную теорему о среднем, получаем
$$
frac{1}{Delta x} (U(x + Delta x, y)-U(x, y)) = P(x + theta Delta x, y), mbox{где} 0 < theta < 1.nonumber
$$

Воспользовавшись непрерывностью функции (P(x, y)) и переходя к пределу при (Delta x rightarrow 0), получаем
$$
lim_{Delta x rightarrow 0} frac{U(x + Delta x, y)-U(x, y)}{Delta x} = P(x, y) = frac{partial U}{partial x}.nonumber
$$

Аналогично доказывается, что (displaystylefrac{partial U}{partial y} = Q(x, y)).

Так как (P(x, y)) и (Q(x, y)) — непрерывные в области (G) функции, то функция (U(x, y)) непрерывно дифференцируема в области (G).
Докажем, что (3. Rightarrow 1.) Это следует из более общего утверждения: если (P(x, y) dx + Q(x, y) dy = dU), то для любого кусочно гладкого контура (gamma) справедливо равенство (displaystyleintlimits_{gamma} P dx + Q dy = 0). Действительно, если (x = x(t), y = y(t), alpha leq t leq beta), есть уравнение кривой (gamma), то
$$
intlimits_{gamma} P dx + Q dy = intlimits_{alpha}^{beta} [P(x(t), y(t))x'(t) + Q(x(t), y(t))y'(t)] dt =\= intlimits_{alpha}^{beta} left[frac{partial U}{partial x} (x(t), y(t))x'(t) + frac{partial U}{partial y} Q(x(t), y(t))y'(t)right] dt =\= intlimits_{alpha}^{beta} frac{d}{dt} [U(x(t), y(t))] dt = U(x(beta), y(beta))-U(x(alpha), y(alpha)) = 0,nonumber
$$
так как начало и конец замкнутой кривой совпадают. (bullet)

Следствие.

Если (displaystyleintlimits_{gamma} P dx + Q dy) равен нулю по любой замкнутой ломаной, то этот интеграл равен нулю и по любому кусочно гладкому контуру (gamma).

(circ) Пусть (displaystyleintlimits_{L} P dx + Q dy = 0) для любой замкнутой ломаной (L). Тогда существует потенциал (U(x, y)) и
$$
P dx + Q dy = frac{partial U}{partial x} (x, y) dx + frac{partial U}{partial y} (x, y) dy.nonumber
$$

Следовательно, (displaystyleintlimits_{gamma} P dx + Q dy = 0). (bullet)

Теорема 1 не дает практического способа для выяснения вопроса о потенциальности поля (P, Q). Для односвязной области (G) докажем эффективный критерий, основанный на использовании формулы Грина.

Теорема 2.

Для того чтобы дифференцируемое в области (G) поле было потенциальным, необходимо, а в случае односвязной области и достаточно, чтобы выполнялось условие
$$
frac{partial P(x, y)}{partial y} = frac{partial Q(x, y)}{partial x}.label{ref6}
$$

Доказательство.

(circ) Необходимость. Пусть поле ((P(x, y), Q(x, y))) непрерывно дифференцируемо и потенциально. Тогда
$$
P(x, y) = frac{partial U(x, y)}{partial x},quad Q(x, y) = frac{partial U(x, y)}{partial y},nonumber
$$
откуда
$$
frac{partial Q(x, y)}{partial x} = frac{partial^{2} U(x, y)}{partial x partial y},quad frac{partial P(x, y)}{partial y} = frac{partial^{2} U(x, y)}{partial y partial x}.nonumber
$$

Так как производные (partial P/partial y) и (partial Q/partial x) непрерывны, то смешанные производные (U_{xy}), (U_{yx}) также непрерывны, а следовательно, равны. Условие eqref{ref6} выполнено в области (G).

Достаточность. Пусть поле (P, Q) задано в односвязной области (G subset boldsymbol{R}^{2}) и выполнено условие eqref{ref6}.

Возьмем произвольную простую замкнутую ломаную (L subset G). Так как область (G) односвязна, то ограничиваемая ломаной (L) область (Omega subset G) и к ней применима формула Грина
$$
intlimits_{L} P dx + Q dy = intlimits_{Omega} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = 0.label{ref7}
$$

Таким образом, интеграл eqref{ref7} равен нулю для любой простой замкнутой ломаной (L).

Теперь нетрудно показать, что интеграл eqref{ref7} равен нулю для любой замкнутой ломаной (даже имеющей точки самопересечения).

Для трехзвенной ломаной интеграл eqref{ref7} всегда равен нулю, если эта ломаная замкнута. Если три ее вершины не лежат на одной прямой, то трехзвенная ломаная будет простой и по доказанному интеграл eqref{ref7} равен нулю. Если же все три вершины лежат на одной прямой, то и в этом случае, как легко видеть, интеграл равен нулю (рис. 51.8).

Рис. 51.8

То, что интеграл eqref{ref7} равен нулю для любой (n)-звенной замкнутой ломаной, докажем индукцией по числу звеньев ломаной.

Пусть выполнено условие eqref{ref6} и интеграл eqref{ref7} равен нулю по любой замкнутой ломаной, число звеньев которой меньше, чем (n). Покажем тогда, что криволинейный интеграл eqref{ref7} равен нулю и по любой замкнутой (n)-звенной ломаной. Если ломаная (L(A_{1}, A_{2}, ldots, A_{n}, A_{1})) простая, то это уже доказано. Пусть у (L) есть точки самопересечения. Предположим, что два звена, (A_{1}A_{2}) и (A_{k}A_{k + 1}), пересекаются. Тогда либо они пересекаются в единственной точке В (рис. 51.8), либо эти два звена пересекаются по целому отрезку. В этом случае точки (A_{1}), (A_{2}), (A_{k}), (A_{k + 1}) лежат на одной прямой (рис. 51.9).

Рис. 51.9

Рассмотрим первый случай. За последующими рассуждениями проще следить по рис. 51.9. В случаях а) и б) ломаная (L) будет объединением замкнутых ломаных (L_{1}(B, A_{k + 1}, ldots, A_{n}, A_{1}, B)) и (L_{2}(B, A_{2}, ldots, A_{k}, B)). Количество звеньев (L_{1}) и (L_{2}) меньше (n). По предположению индукции интеграл eqref{ref7} по каждой из этих ломаных равен нулю. Следовательно, он равен нулю и по их объединению — ломаной (L).

Аналогично рассматривается и второй случай, когда точки (A_{1}), (A_{2}), (A_{k}), (A_{k + 1}) лежат на одной прямой и отрезки (A_{1}A_{2}) и (A_{k}A_{k + 1}) пересекаются. Без ограничения общности можно считать, что точка (A_{k}) лежит на отрезке (A_{1}A_{2}). Тогда (L) есть объединение замкнутых ломаных (L_{1}(A_{k}, A_{k + 1}, ldots, A_{n}, A_{1}, A_{k})) и (L_{2}(A_{k}, A_{2}, ldots, A_{k-1}, A_{k})), имеющих меньше, чем (n) звеньев. Интеграл eqref{ref7} по (L_{1}) и (L_{2}) равен нулю. Следовательно, он равен нулю и по ломаной (L).

Так как интеграл eqref{ref7} равен нулю по любой замкнутой ломаной (L subset G), то в силу теоремы 1 поле ((P, Q)) будет потенциальным. (bullet)

Заметим, что условие односвязности области существенно для справедливости теоремы 2. Подтвердим это следующим примером.

Пример 2.

Показать, что непрерывно дифференцируемое при (x^{2} + y^{2} > 0) плоское векторное поле
$$
P(x, y) = -frac{omega}{2pi} frac{y}{x^{2} + y^{2}},quad Q(x, y) = frac{omega}{2pi} frac{x}{x^{2} + y^{2}}label{ref8}
$$
удовлетворяет условию eqref{ref6}, но не является потенциальным при (omega neq 0).

Решение.

(vartriangle) Условие eqref{ref6} выполняется, так как
$$
frac{partial P}{partial y} = frac{omega}{2pi} frac{y^{2}-x^{2}}{(y^{2} + x^{2})^{2}} = frac{partial Q}{partial x}.nonumber
$$

Рассмотрим окружность (C_{R}), заданную уравнениями (x = R cos t), (y = R sin t), (0 leq t leq 2pi). Тогда
$$
intlimits_{C_{R}} P dx + Q dy = frac{omega}{2pi} intlimits_{C_{R}} frac{x dy-y dx}{x^{2} + y^{2}} = frac{omega}{2pi} intlimits_{0}^{2pi} dt = omeganonumber
$$
и в силу теоремы 1 поле ((P, Q)) не может быть потенциальным.

Теорема 2 неприменима, поскольку поле определено в неодносвязной области (G = {(x, y): x^{2} + y^{2} > 0}). (blacktriangle)

Рис. 51.10

Замечание

В гидродинамике поле eqref{ref8} интерпретируется как поле скоростей точечного вихря, расположенного в точке ((0, 0)) и имеющего интенсивность (omega). Если перейти к полярным координатам (r), (varphi), то
$$
v = (p, Q) = frac{omega}{2pi r} (-sin varphi, cos varphi).nonumber
$$
Жидкие частицы вращаются по концентрическим окружностям с постоянными скоростями, обратно пропорциональными расстоянию от точечного вихря (рис. 51.10).

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2019 года; проверки требуют 5 правок.

Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру и двойным интегралом по односвязной области , ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина.

Формулировка[править | править код]

Пусть — положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а — область, ограниченная кривой . Если функции , определены в области и имеют непрерывные частные производные $frac{partial P}{partial y}$ , $frac{partial Q}{partial x}$ , то

$ointlimits_{C} P ,dx + Q ,dy = iintlimits_{D} left( frac{partial Q}{partial x} - frac{partial P}{partial y} right) ,dx,dy$

На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая замкнута.

Доказательство для простой области[править | править код]

— область, правильная в направлении , ограниченная замкнутой кривой

Пусть область — криволинейная трапеция (область, правильная в направлении ):

$D = { (x,y)|a le x le b, y_1(x) le y le y_2(x) }$

Для кривой , ограничивающей область зададим направление обхода по часовой стрелке.

Тогда:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = intlimits_{a}^{b}dx intlimits_{y_1(x)}^{y_2(x)} frac{partial P}{partial y} ,dy = intlimits_{a}^{b} (P(x,y_2(x)) - P(x,y_1(x))) ,dx =$

$= intlimits_{a}^{b} P(x,y_2(x)) ,dx - intlimits_{a}^{b} P(x,y_1(x)) ,dx quad (1)$

Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:

$intlimits_{C_1} P(x,y) ,dx = -intlimits_{-C_1} P(x,y) ,dx = -intlimits_{a}^{b} P(x,y_1(x)) ,dx quad (2)$

$intlimits_{C_3} P(x,y) ,dx = intlimits_{a}^{b} P(x,y_2(x)) ,dx quad (3)$

Интеграл по $C_{1}$ берётся со знаком «минус», так как согласно ориентации контура направление обхода данной части — от до .

Криволинейные интегралы по $C_{2}$ и $C_{4}$ будут равны нулю, так как :

$intlimits_{C_2} P(x,y) ,dx = 0 quad (4)$

$intlimits_{C_4} P(x,y) ,dx = 0 quad (5)$

Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = intlimits_{C_1} P(x,y) ,dx + intlimits_{C_3} P(x,y) ,dx + intlimits_{C_2} P(x,y) ,dx + intlimits_{C_4} P(x,y) ,dx$

Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой в отрицательном направлении:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = -intlimits_{C} P(x,y) ,dx quad (6)$

Аналогично доказывается формула:

$iintlimits_{D} frac{partial Q}{partial x} ,dx,dy = intlimits_{C} Q(x,y) ,dy quad (7)$

если в качестве области взять область, правильную в направлении .

Складывая (6) и (7), получим:

$intlimits_{C} P ,dx + Q ,dy = iintlimits_{D} left( frac{partial Q}{partial x} - frac{partial P}{partial y} right) ,dx,dy$

Формулы Грина[править | править код]

Если бы в электростатических задачах мы всегда имели дело с дискретным или непрерывным распределением заряда без всяких граничных поверхностей, то общее решение для скалярного потенциала

$Phi (x)=int {frac {rho (x')}{|x-x'|}}d^{3}x$

было бы самой удобной и непосредственной формой решения таких задач и не нужны были бы ни уравнение Лапласа, ни уравнение Пуассона. Однако
в действительности в целом ряде, если не в большинстве, задач электростатики мы имеем дело с конечными областями пространства (содержащими или не содержащими заряд), на граничных поверхностях которых заданы определённые граничные («краевые») условия. Эти граничные условия могут быть заменены некоторым соответственно подобранным распределением зарядов вне рассматриваемой области (в частности, в бесконечности), однако приведённое выше соотношение в этом случае уже непригодно для расчёта потенциала, за исключением некоторых частных случаев (например, в методе изображений).

Для рассмотрения задач с граничными условиями необходимо расширить используемый нами математический аппарат, а именно вывести так называемые формулы, или теоремы Грина (1824 г.).
Они получаются непосредственно из теоремы о дивергенции

$intlimits_V operatorname{div}~A,d^3x=ointlimits_S A cdot n,da$

которая справедлива для любого векторного поля А, определённого в объёме V, ограниченном замкнутой поверхностью S. Пусть , где varphi и psi — произвольные дважды непрерывно-дифференцируемые скалярные функции.
Тогда

$operatorname{div} , (varphi ; operatorname{grad} , psi)=varphi nabla^2 psi + operatorname{grad} ~varphi cdot operatorname{grad} ~psi qquad (1)$

$varphi ; operatorname{grad} , psi cdot n=varphi frac{partial psi}{partial n} qquad (2)$

где $frac{partial}{partial n}$ — нормальная производная на поверхности S (по
направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина

$intlimits_V (varphi ; nabla^2 psi + operatorname{grad} , varphi cdot operatorname{grad} , psi),d^3x = ointlimits_S varphi frac{partial psi}{partial n} ,da qquad (3)$

Напишем такую же формулу, поменяв в ней местами varphi и psi ,
и вычтем её из (3). Тогда члены с произведением
сократятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина:

$intlimits_V (varphi nabla^2 psi - psi nabla^2 varphi),d^3x = ointlimits_S left[varphi frac{partial psi}{partial n} - psi frac{partial varphi}{partial n}right] ,da$

В физике и математике теорема Грина дает соотношение между криволинейным интегралом простой ограниченной кривой С и двойным интегралом по плоской поверхности D ограниченной кривой С. И в общем виде записывается следующим образом

$intlimits_{C} L, dx + M, dy = iintlimits_{D} left(frac{partial M}{partial x} - frac{partial L}{partial y}right), dA.$

В физике Теорема Грина в основном используется для решения двумерных потоковых интегралов, исходя из того, что сумма исходящих потоков в любой точке области равна результирующему потоку, суммируемому по всей ограничивающей поверхности.

Третья формула Грина получается из второй путём замены $psi = frac{1}{|mathbf{x} - mathbf{y}|}$ и замечания о том, что $nabla^2 psi = - 4 pi delta left( mathbf{x} - mathbf{y} right)$ в ${{mathbb{R}}^{3}}$ . Если дважды дифференцируема на U.

$ointlimits_{partial U} left[ {1 over |mathbf{x} - mathbf{y}|} {partial phi over partial n} (mathbf{y}) - phi(mathbf{y}) {partial over partial n_mathbf{y}} {1 over |mathbf{x} - mathbf{y}|}right], dS_mathbf{y} - intlimits_U left[ {1 over |mathbf{x} - mathbf{y}|} nabla^2 phi(mathbf{y})right], dV_mathbf{y} = k$

если (здесь Int обозначает внутренность множества),

если
и в точке к граничной поверхности имеется касательная плоскость.

См. также[править | править код]

Дельта-функция
Теорема Стокса
Формула Остроградского
Дискретная теорема Грина

Литература[править | править код]

Д. Ж. Джексон Классическая электродинамика (1965 г.)
Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977. — 735 с.

Источник

Лекция 6. Формула Грина.

Теорема (формула) Грина. Пусть G – плоская односвязная область с кусочно-гладкой границей L. Пусть функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в области G и на L.

Тогда справедлива формула Грина

Доказательство. 1) Назовем плоскую область D (в плоскости OXY) правильной, если любая прямая, параллельная координатной оси (OX или OY) пересекает область не более, чем в двух точках. Можно показать, что область G можно представить как объединение конечного числа правильных областей .

Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям. Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании.

Поэтому доказательство может быть проведено для правильной области G.

2) Пусть G – правильная область. Так как P, Q могут быть произвольными функциями, то формула Грина сводится двум формулам и , каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.

Рекомендуемые материалы

FREE

ТФКП Первое ДЗ 16 Вариант 1-5 номера

Портфель состоит из двух активов, ожидаемая доходность и риск (в процентах) которых равны А (18, 6) и В (10, 5). Коэффициент корреляции активов А и В равен -0,5. Найти портфель минимального риска, его риск и доходность.

Фирма имеет ряд финансовых обязательств перед одним кредитором – S1 = 2 млн. рублей, S2 = 3 млн. рублей и S3 = 2,5 млн. рублей, которые должна погасить соответственно через n1 = 170, n2 = 235, n3 = 270 дней после 01.01 текущего года (K= 365дней). По

FREE

Для приема зачета заготовлено 100 задач: 60 — по теории вероятности и 40 — по математической статистике. Для получения зачета студент должен решить одну из предложенных задач. Известно, что он умеет решать 40 задач по теории вероятности и 30 задач —

FREE

5 и 6 задачи из 2-го типаря

Вычисление площади области по формуле Грина.

По свойству 3 двойного интеграла площадь области D можно вычислить по формуле

. Поэтому достаточно выбрать P, Q так, чтобы , чтобы с помощью криволинейного интеграла по формуле Грина можно было бы вычислять площадь области.

Например, можно выбрать Q=x, P=0. Тогда . Можно выбрать Q=0, P=y, тогда . Очень полезна бывает симметричная формула при .

Пример. Вычислить площадь эллипса с полуосями a, b

Полный дифференциал и его вычисление.

Теорема (о полном дифференциале). Для того чтобы выражение — было полным дифференциалом некоторой функции — потенциала, необходимо и достаточно, чтобы в условиях формулы Грина было выполнено одно из следующих четырех условий (эквивалентных условий полного дифференциала)

1) зависит только от начальной A и конечной B точек дуги и не зависит от формы дуги (не зависит от пути интегрирования),

2) для любого кусочно-гладкого контура

3) ,

4) .

Доказательство. Схема доказательства теоремы . По этой цепочке можно последовательно добраться от любого пункта к любому другому.

Дополнительно предположим, что существуют и непрерывны вторые смешанные производные функции V. Тогда они равны.

. Это следует из формулы Грина.

. Пусть точки A, B соединены двумя дугами L₁ и L₂. Тогда из них можно составить контур , интеграл вдоль которого по п.2 равен нулю.

== —

. Поэтому =.

. Докажем, что — потенциал, то есть, что

. Докажем первое соотношение, второе доказывается аналогично.

Заметим, что такая запись интеграла показывает, что интеграл не зависит от формы дуги. Поэтому мы можем в первом интеграле провести дугу через точку (x, y), чтобы в первом и втором интеграле сократились интегралы по дуге, соединяющей начальную точку с точкой (x, y). В первом интеграле выберем в качестве дуги, соединяющей точку (x, y) с точкой (x+Dx) отрезок прямой, параллельный оси OX. На этом отрезке y не изменяется, поэтому dy=0

Тогда, продолжая равенство, получим

= =

(здесь мы перешли от криволинейного интеграла к определенному, так как дуга интегрирования – отрезок, параллельный оси OX и применили теорему о среднем для определенного интеграла). Теперь используем непрерывность функции P(x, y) по переменной x.

= . Первое соотношение доказано.

Для доказательства второго соотношения варьируется переменная y, дуга, соединяющая точки (x_0,y₀), и (x, y+Dy) проводится через точку (x, y) и далее по отрезку, параллельному оси OY, соединяющему точки (x, y) и (x, y+Dy).

Формула Ньютона – Лейбница.

Пусть выполнены условия теоремы о полном дифференциале и пусть выражение

— полный дифференциал, а функция — потенциал.

Тогда справедлива формула Ньютона – Лейбница

, где — потенциал.

Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде . Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x₁, y₁), (x₂, y₂) можно провести через точку (x₀, y₀). Поэтому = + = — = .

Теорема (о полном дифференциале) для пространственной кривой.

Пусть дуга AB лежит на кусочно-гладкой поверхности S, пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны и имеют непрерывные частные производные на S. Тогда следующие четыре утверждения эквивалентны.

1) не зависит от формы дуги (от пути интегрирования), а зависит только от начальной и конечной точек дуги.

2) Для любого замкнутого контура

4) . — полный дифференциал.

Доказательство. Доказательство аналогично двумерному случаю, схема доказательства та же: . Докажите ее самостоятельно.

проводится по теореме о смешанных производных так же как в двумерном случае.

проводится по теореме Стокса (будет сформулирована и доказана ниже).

доказательство полностью аналогично двумерному случаю.

доказательство аналогично двумерному случаю.

Замечание. Формула Ньютона-Лейбница справедлива в трехмерном случае и доказывается так же.

Вычисление криволинейного интеграла от полного дифференциала.

Криволинейный интеграл от полного дифференциала можно вычислять двумя способами.

1) Можно выбирать удобный путь интегрирования, например, состоящий из отрезков, параллельных OX и OY. На отрезке, параллельном OX, dy=0, так как y не изменяется на этом отрезке. На отрезке, параллельном OY, dx=0, так как x не изменяется на этом отрезке. Тогда = +

2) Можно восстановить потенциал, как это делалось на первом курсе при решении дифференциальных уравнений в полных дифференциалах и применить формулу Ньютона-Лейбница.

Пример. Вычислить интеграл .

1) =

Сравнивая две записи потенциала, получим .

Заметим, что аналогично вычисляется криволинейный интеграл от полного дифференциала по пространственной кривой.

Формула Грина для многосвязной области.

Пусть кусочно-гладкие контуры лежат внутри контура и вне друг друга. Пусть непрерывны и имеют непрерывные частные производные по переменным x, y в области между контурами и на самих этих контурах. Тогда

Складывая интегралы, получим

Рекомендация для Вас — 5. Частотные характеристики систем.

Отсюда имеем

= . Теорема доказана для случая n = 2. Для n > 2 доказательство аналогично.

Следствие 1. Пусть Pdx+Qdy – полный дифференциал и n=1.

Тогда. Поэтому, если в какой-либо точке нарушается непрерывность функций, P, Q или их частных производных, то интеграл может быть взят по любому кусочно-гладкому не самопересекающемуся контуру, охватывающему эту точку (мы получим один и тот же результат).

Следствие 2. Пусть Pdx+Qdy – полный дифференциал Если кусочно-гладкий контур один раз охватывает некоторую точку, , а контур L n раз охватывает эту точку, то в условиях теоремы . Докажите это самостоятельно.

Источник

16.3.3.4.1. Связность,
односвязность, многосвязность. Напомним
определения ряда понятий из теории
функций нескольких переменных, которыми
нам придется пользоваться.

Множество точек
(на прямой, на плоскости, в пространстве)
называется связным,
если любые две точки этого множества
можно соединить непрерывной кривой,
целиком принадлежащей этому множеству.

Область (на
плоскости, в пространстве) называется
односвязной,
если любой замкнутый контур, лежащий в
этой области, можно непрерывной
деформацией стянуть в точку, не выходя
при этом за пределы области.

Примеры: односвязны
шар, параллелепипед и вообще любой
выпуклый объём в пространстве. Односвязен
шаровой слой, заключённый между двумя
сферами. Пример неодносвязной области:
тор. Все пространство односвязно и
остаётся односвязным, если из него
удалить точку или отрезок. Если же
удалить из пространства прямую, оно
потеряет свойство односвязности:
окружность, охватывающую эту прямую,
не удастся стянуть в точку, не пересекая
прямую.

Кусочно-гладкая
граница ограниченной односвязной
области всегда связна, следовательно,
является контуром.

16.3.3.4.2. Теорема
Грина для односвязной области. Пусть
на плоскости Oxy
задана односвязная область
D,
ограниченная кусочно-гладким контуром
C.
На множестве

определены непрерывные функции

и
,
имеющие непрерывные частные производные.
Тогда
,
при этом контур
С обходится
так, что область D
остаётся слева.

Док-во.
1. Пусть D
— простая область. Докажем сначала, что

.
ОпишемD
неравенствами
Тогда

.
Если контур включает вертикальные
участки, такие как EF,
то на этих участках dx=
0, поэтому
,
и
,
что и требовалось доказать.

Равенство

доказывается точно также:

.
Суммируя равенства

и
,
получим одну из важнейших формул анализа
-формулу Грина

2.
Пусть теперьD
— произвольная, не обязательно простая,
область. Разобьём её на простые части.
Пусть это разбиение производится
отрезком АВ,
и пусть подобласти D₁
и D₂
— результат разбиения. Для этих подобластей
формула Грина доказана:

и .
По свойству аддитивности ,

.
Суммируя эти выражения, убеждаемся, что
криволинейные интегралы по отрезкамАВ
и ВА
взаимно уничтожаются, а сумма интегралов
по кривым ВFA
и AEB
даёт интеграл по контуру С,
т.е. формула Грина верна и для области,
не являющейся простой. Доказательство
остаётся справедливым и в случае, когда
разбиение производится добавлением
большего числа, чем одна, кривых.

16.3.3.4.3.
Теорема Грина для многосвязной области.
Пусть теперь
D
многосвязная на плоскости Oxy.
Граница многосвязной области состоит
из нескольких связных частей, не имеющих
общих точек. Рассмотрим случай, когда
граница области D
(на рисунке область заштрихована) состоит
из внешнего контура С
и внутренних контуров С₁
и С₂.
Соединим контур С
разрезом
FM
с контуром С₁,
разрезом BG
— с контуром С₂.
(Под словами «соединим разрезом BG
» подразумевается то, что мы удалим
из D
отрезок BG).
Область
с границей
односвязна, поэтому для неё справедлива
формула Грина:

.
Двойные интегралы по областям D
и

равны
(площадь разрезов равна нулю); в
криволинейный интеграл по кусочно-гладкой
кривой

интегралы по разрезам входят с
противоположными знаками (
и
,
например) и поэтому взаимно уничтожаются,
поэтому оказывается справедлива теорема
Грина для многосвязной области: пусть
на плоскости Oxy
дана многосвязная область
D
с границей

.
На множестве

определены непрерывные функции

и
,
имеющие непрерывные частные производные.
Тогда
,
при этом каждая часть полной границы

обходится так, что область D
остаётся слева.

16.3.3.5.
Условия независимости криволинейного
интеграла от пути интегрирования. В
этом разделе будет дан ответ на вопрос:
при каких условиях криволинейный
интеграл второго рода

не зависит от формы пути, соединяющего
точки А
и В,
а определяется только этими точками?
Будем предполагать, что в некоторой
односвязной области
на плоскости заданы непрерывно
дифференцируемые функции

и
,
и все рассматриваемые точки, контуры и
области принадлежат этой области.

16.3.3.5.1.
Теорема 1. Для
того, чтобы интеграл

не зависел от формы пути, соединяющего
точки А
и В,
необходимо и достаточно, чтобы интеграл
по любому замкнутому контуру был равен
нулю.

Доказательство.
Необходимость.
Пусть
— произвольный замкнутый контур, лежащий
в области ,
А
и В
— произвольные точки этого контура. Так
как, по условию, ,
то
.

Достаточность.
Пусть для любого контура
выполняется .
Пусть ,

— произвольные точки,
и
— две различных кривых, соединяющих эти
точки.
— замкнутый контур, поэтому

,
что и требовалось доказать.

16.3.3.5.2. Теорема
2. Для того,
чтобы интеграл

по любому контуру С
был равен нулю, необходимо и достаточно,
чтобы функции
и их частные производные были непрерывны,
и выполнялось условие.

Доказательство.
Необходимость.
От противного. Пусть для
выполняется
,
но существует точка
такая, что .
Предположим для определённости, что .
Так как разность
непрерывна, существует окрестность
точки
такая, что .
Выберем контур С,
целиком лежащий в этой окрестности.
Если D
— область ограниченная этим контуром,
то, по формуле Грина, .
Но, по теореме об интегрировании
неравенств,
(
— площадь области D),
т.е. ,
что противоречит условиям теоремы.
Следовательно, в любой точке
выполняется условие .

Достаточность.
Если в любой точке
выполняется условие ,
то для любого контура С

(D
— область ограниченная контуром С).

Таким образом, для
того, чтобы криволинейный интеграл

не зависел от формы пути, соединяющего
начальную и конечную точки (или, что то
же самое, интеграл по любому замкнутому
контуру был равен нулю), требуется
выполнение двух условий:

Контур и ограниченная
им область лежат в некоторой односвязной
области, в которой
и их частные
производные непрерывны , и.

Отметим существенность
первого условия. Так, для интеграла
второе условие выполняется: ,
в то же время интеграл по окружности
радиуса R
не равен нулю: .
Причина — функции Р
и Q
непрерывны всюду, кроме начала координат;
удаление точки из плоскости лишает её
свойства односвязности.

Источник

Формула Грина

Формула Грина на плоскости

Ориентация границы плоской области.

Формула Грина.

Формула Грина для многосвязной области.

Применение формулы Грина к вычислению площадей.

Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).

Формулировка[править | править код]

Доказательство для простой области[править | править код]

Формулы Грина[править | править код]

См. также[править | править код]

Литература[править | править код]

Рекомендуемые материалы

Добавить комментарий Отменить ответ