Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2019 года; проверки требуют 5 правок.
Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру 

Формулировка[править | править код]
Пусть 







На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая 
Доказательство для простой области[править | править код]


Пусть область 

Для кривой 

Тогда:
Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:
Интеграл по 



Криволинейные интегралы по 


Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:
Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой 
Аналогично доказывается формула:
если в качестве области 

Складывая (6) и (7), получим:
Формулы Грина[править | править код]
Если бы в электростатических задачах мы всегда имели дело с дискретным или непрерывным распределением заряда без всяких граничных поверхностей, то общее решение для скалярного потенциала
было бы самой удобной и непосредственной формой решения таких задач и не нужны были бы ни уравнение Лапласа, ни уравнение Пуассона. Однако
в действительности в целом ряде, если не в большинстве, задач электростатики мы имеем дело с конечными областями пространства (содержащими или не содержащими заряд), на граничных поверхностях которых заданы определённые граничные («краевые») условия. Эти граничные условия могут быть заменены некоторым соответственно подобранным распределением зарядов вне рассматриваемой области (в частности, в бесконечности), однако приведённое выше соотношение в этом случае уже непригодно для расчёта потенциала, за исключением некоторых частных случаев (например, в методе изображений).
Для рассмотрения задач с граничными условиями необходимо расширить используемый нами математический аппарат, а именно вывести так называемые формулы, или теоремы Грина (1824 г.).
Они получаются непосредственно из теоремы о дивергенции
-
,
которая справедлива для любого векторного поля А, определённого в объёме V, ограниченном замкнутой поверхностью S. Пусть 


Тогда
и
-
,
где 
направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина
-
.
Напишем такую же формулу, поменяв в ней местами 

и вычтем её из (3). Тогда члены с произведением
сократятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина:
-
.
В физике и математике теорема Грина дает соотношение между криволинейным интегралом простой ограниченной кривой С и двойным интегралом по плоской поверхности D ограниченной кривой С. И в общем виде записывается следующим образом
В физике Теорема Грина в основном используется для решения двумерных потоковых интегралов, исходя из того, что сумма исходящих потоков в любой точке области равна результирующему потоку, суммируемому по всей ограничивающей поверхности.
Третья формула Грина получается из второй путём замены 






и в точке 
См. также[править | править код]
- Дельта-функция
- Теорема Стокса
- Формула Остроградского
- Дискретная теорема Грина
Литература[править | править код]
- Д. Ж. Джексон Классическая электродинамика (1965 г.)
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977. — 735 с.
Формула Грина
Связность, односвязность, многосвязность
Напомним определения ряда понятий из теории функций нескольких переменных, которыми нам придется пользоваться.
Множество точек { на прямой, на плоскости, в пространстве } называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.
Область { на плоскости, в пространстве } называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области.
Примеры:
Односвязны шар, параллелепипед и вообще любой выпуклый объём в пространстве. Односвязен шаровой слой, заключённый между двумя сферами. Пример неодносвязной области: тор. Все пространство односвязно и остаётся односвязным, если из него удалить точку или отрезок. Если же удалить из пространства прямую, оно потеряет свойство односвязности: окружность, охватывающую эту прямую, не удастся стянуть в точку, не пересекая прямую.
Кусочно-гладкая граница ограниченной односвязной области всегда связна, следовательно, является контуром.
Теорема Грина для односвязной области
Пусть на плоскости $mathbf { textit { Oxy } } $ задана односвязная область$mathbf { textit { D } } $, ограниченная кусочно-гладким контуром $mathbf { textit { C } } $. На множестве $bar { D } =Dcup C$ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные.
Тогда $ointlimits_С { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $, при этом контур$mathbf { textit { C } } $ обходится так, что область $mathbf { textit { D } } $ остаётся слева.
Доказательство
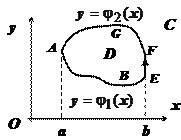
1). Пусть $mathbf { textit { D } } $ — простая область. Докажем сначала, что $ointlimits_C { P(x,y)dy } =-iintlimits_D { frac { partial P } { partial y } dxdy } $.
$y=varphi _2 (x)y=varphi _1 (x)$
Опишем $mathbf{textit{D}}$ неравенствами $D:left({begin{array}{l} aleqslant xleqslant b, \ varphi _1 (x)leqslant yleqslant varphi _2 (x). \ end{array}}right.$
Тогда $-iintlimits_D { frac { partial P } { partial y } dxdy } =-intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _x (x) } { frac { partial P } { partial y } dy } } =-intlimits_a^b { left. { P(x,y) }right|_ { varphi _1 (x) } ^ { varphi _2 (x) } dx } =-intlimits_a^b { P(x,varphi _2 (x))dx } — +intlimits_a^b { P(x,varphi _1 (x))dx } = \ =intlimits_a^b { P(x,varphi _1 (x))dx } -intlimits_b^a { P(x,varphi _2 (x))dx } =intlimits_ { mathop { ABE } limits^cup } { P(x,y)dx } + intlimits_ { mathop { FGA } limits^cup } { P(x,y)dx } $.
Если контур включает вертикальные участки, такие как $mathbf { textit { EF } } $, то на этих участках $mathbf { textit { dx } } = 0$, поэтому $intlimits_ { mathop { EF } limits^cup } { P(x,y)dx } =0$, и $y=psi _2 (y)y=psi _1 (y)-iintlimits_D { frac { partial P } { partial y } dxdy } =intlimits_ { mathop { ABE } limits^cup } { P(x,y)dx } +intlimits_ { mathop { EF } limits^cup } { P(x,y)dx } +intlimits_ { mathop { FGA } limits^cup } { P(x,y)dx } =ointlimits_C { P(x,y)dx } $, что и требовалось доказать.
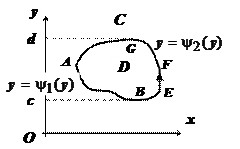
Равенство $ointlimits_C { Q(x,y)dy } =iintlimits_D { frac { partial Q } { partial x } dxdy } $ доказывается точно также:
$iintlimits_D { frac { partial Q } { partial x } dxdy } =intlimits_c^d { dyintlimits_ { psi _1 (y) } ^ { psi _2 (y) } { frac { partial Q } { partial x } dx } } =intlimits_c^d { left. { Q(x,y) }right|_ { psi _1 (y) } ^ { psi _2 (y) } dy } = intlimits_c^d { Q(psi _2 (y),y)dy } -intlimits_c^d { Q(psi _1 (y),y)dy } = \ = intlimits_ { mathop { BEFG } limits^cup } { Q(x,y)dy } + intlimits_ { mathop { GAC } limits^cup } { Q(x,y)dy } =ointlimits_C { Q(x,y)dy } $.
Суммируя равенства $ointlimits_C { P(x,y)dy } =-iintlimits_D { frac { partial P } { partial y } dxdy } $ и $ointlimits_C { Q(x,y)dy } =iintlimits_D { frac { partial Q } { partial x } dxdy } $, получим одну из важнейших формул анализа — формулу Грина $ ointlimits_С { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $
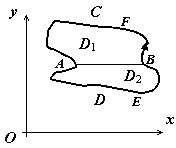
2). Пусть теперь $mathbf { textit { D } } $ — произвольная, не обязательно простая, область. Разобьём её на простые части. Пусть это разбиение производится отрезком $mathbf { textit { АВ } } $ и пусть подобласти $mathbf { textit { D } } _ { 1 } $ и $mathbf { textit { D } } _ { 2 } $ — результат разбиения. Для этих подобластей формула Грина доказана:
$ointlimits_ { ABFA } { Pdx+Qdy=iintlimits_ { D_1 } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $ и $ointlimits_ { AEBA } { Pdx+Qdy=iintlimits_ { D_2 } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $.
По свойству аддитивности $ointlimits_ { ABFA } { Pdx+Qdy } =ointlimits_ { AB } { Pdx+Qdy } +ointlimits_ { BFA } { Pdx+Qdy } $, $ointlimits_ { AEBA } { Pdx+Qdy } =ointlimits_ { AEB } { Pdx+Qdy } +ointlimits_ { BA } { Pdx+Qdy } = ointlimits_ { AEB } { Pdx+Qdy } -ointlimits_ { AB } { Pdx+Qdy } $
Суммируя эти выражения, убеждаемся, что криволинейные интегралы по отрезкам $mathbf { textit { АВ } } $ и $mathbf { textit { ВА } } $ взаимно уничтожаются, а сумма интегралов по кривым $mathbf { textit { BFA } } $ и $mathbf { textit { AEB } } $ даёт интеграл по контуру $mathbf { textit { C } } $, т.е. формула Грина верна и для области, не являющейся простой.
Доказательство остаётся справедливым и в случае, когда разбиение производится добавлением большего числа, чем одна, кривых.
Теорема Грина для многосвязной области
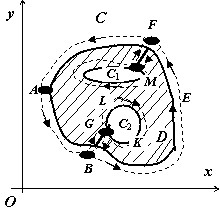
Пусть теперь $mathbf { textit { D } } $ многосвязная на плоскости $mathbf { textit { Oxy } } $. Граница многосвязной области состоит из нескольких связных частей, не имеющих общих точек.
Рассмотрим случай, когда граница области $mathbf { textit { D } } $ { на рисунке область заштрихована } состоит из внешнего контура $mathbf { textit { C } } $ и внутренних контуров $mathbf { textit { C } } _ { 1 } $ и $mathbf { textit { C } } _ { 2 } $.
Соединим контур $mathbf { textit { C } } $разрезом $mathbf { textit { FM } } $ с контуром $mathbf { textit { C } } _ { 1 } $, разрезом $mathbf { textit { BG } } $ — с контуром $mathbf { textit { C } } _ { 2 } $. { Под словами «соединим разрезом $mathbf { textit { BG } } $ » подразумевается то, что мы удалим из $mathbf { textit { D } } $ отрезок $mathbf { textit { BG } } )$.
Область $ { D } ‘=Dbackslash (BGcup FM)$ с границей $ { Gamma } ‘=mathop { AB } limits^cup cup BGcup (C_2 =mathop { GLKG } limits^cup )cup GBcup mathop { BF } limits^cup cup FMcup C_1 cup MFcup mathop { MA } limits^cup $ односвязна, поэтому для неё справедлива формула Грина:
$ointlimits_ { { Gamma } ‘ } { Pdx+Qdy=iintlimits_ { { D } ‘ } { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $
Двойные интегралы по областям $mathbf { textit { D } } $ и $ { D } ‘mathbf { } $ равны { площадь разрезов равна нулю } ; в криволинейный интеграл по кусочно-гладкой кривой $ { Gamma } ‘$ интегралы по разрезам входят с противоположными знаками { $intlimits_ { BG } { Pdx } +Qdy$ и $intlimits_ { GB } { Pdx } +Qdy$, например } и поэтому взаимно уничтожаются, поэтому оказывается справедлива теорема Грина для многосвязной области :
пусть на плоскости $mathbf { textit { Oxy } } $ дана многосвязная область$mathbf { textit { D } } $ с границей $Gamma $. На множестве $bar { D } =Dcup Gamma $ определены непрерывные функции $P(x,y)$ и $Q(x,y)$, имеющие непрерывные частные производные. Тогда $ointlimits_Gamma { P(x,y)dx+Q(x,y)dy=iintlimits_D { left( { frac { partial Q } { partial x } -frac { partial P } { partial y } }right)dxdy } } $, при этом каждая часть полной границы $Gamma $ обходится так, что область $mathbf { textit { D } } $ остаётся слева.
Формула Грина
Формула Грина устанавливает связь между
двойным интегралом по области
и криволинейным интегралом по контуру
,
ограничивающему эту область. Будем
считать, что областьявляется стандартной в направлении
каждой координатной оси и снизу ограничена
графиком функции
(дугой),
сверху — графиком функции
(дугой),
которые вместе составляют замкнутый
контур.
Пусть в области
и на ее границе
заданы функции
и
непрерывные
вместе со своими частными производными
,
,
тогда
,
где обход контура
совершается в положительном направлении,
т. е. против часовой стрелки (областьостается слева). Следовательно,
.
(1)
Аналогично получаем
,
(2)
где обход контура
также совершается в положительном
направлении.
Вычитая почленно (1) из (2), получаем
формулу Грина
.
Замечание 1.Если обход контурасовершается в отрицательном направлении,
т. е. по часовой стрелке (областьостается справа), то формула Грина
принимает вид
.
Замечание 2.Формула Грина дает
возможность вычислять площадь области
с помощью криволинейного интеграла.
Действительно, если,
,
то формула Грина перепишется так:
,
откуда
,
(3)
где обход контура
совершается против часовой стрелки.
Пример. Определить с помощью
криволинейного интеграла площадь,
ограниченную эллипсом с полуосямии
.
Решение.Запишем параметрические
уравнения эллипса
.
Тогда
И по формуле (3) получим
.
Условия независимости криволинейного интеграла от пути интегрирования
Рассмотрим криволинейный интеграл
,
взятый по некоторой плоской
кривой
,
соединяющей точки
и
.
Б
предполагать, что функции
и
имеют непрерывные
частные производные в рассматриваемой
области
.
Выясним, при каких
условиях написанный криволинейный
интеграл не зависит от формы кривой
,
а зависит только
от положения начальной
и конечной точек
и
.
Рассмотрим две произвольные
кривые
и
,
лежащие в рассматриваемой
области
и соединяющие точки
и
.
Пусть
,
(1)
т. е.
.
Тогда на основании свойств 1 и 2
криволинейных интегралов имеем:
,
т. е. криволинейный интеграл
по замкнутому контуру
(2)
В последней формуле
криволинейный интеграл взят по замкнутому
контуру
,
составленному из кривых
и
.
Этот контур
можно, очевидно, считать
произвольным.
Таким образом, из условия,
что для любых двух точек
и
криволинейный интеграл
не зависит от формы соединяющей их
кривой, а зависит только от положения
этих точек, следует, что криволинейный
интеграл по любому замкнутому контуру
равен нулю.
Справедливо и обратное заключение: если
криволинейный интеграл по любому
замкнутому контуру равен нулю, то этот
криволинейный интеграл не зависит от
формы кривой, соединяющей две любые
точки, а зависит только от положения
этих точек. Действительно, из равенства
(2) следует равенство (1).
Естественно возникает
вопрос: каким условиям должны удовлетворять
функции
и
для того, чтобы
криволинейный интеграл по любому
замкнутому контуру был равен нулю. Ответ
на этот вопрос дает следующая теорема:
Теорема.
Пусть во всех точках
некоторой области
функции
и
вместе со своими частными производными
,
непрерывны. Тогда, для того
чтобы криволинейный интеграл по любому
замкнутому контуру
,
лежащему в этой области, был равен нулю,
т. е. чтобы
,необходимо и достаточно
выполнение равенства
(3)
во всех точках области
.
Доказательство.Рассмотрим
произвольный замкнутый контур
в области D и запишем для него формулу
Грина:
.
Если выполняется условие (3), то двойной
интеграл, стоящий слева, тождественно
равен нулю и, следовательно,
Таким образом, достаточность условия
(3) доказана.
Докажем теперь необходимость этого
условия, т.е. докажем, что если равенство
(2) выполняется для любой замкнутой
кривой
в области
,
то в каждой точке этой области выполняется
и условие (3).
Допустим, напротив, что равенство (2)
выполняется, т. е.
,
а условие (3) не выполняется, т. е.
хотя бы в одной точке. Пусть, например,
в некоторой точке
выполняется неравенство
.
Так как в левой части неравенства стоит
непрерывная функция, то она будет
положительна и больше некоторого числа
во всех точках некоторой достаточно
малой области,
содержащей точку.
Возьмем двойной интеграл по этой
области от разности.
Он будет иметь положительное значение.
Действительно,
.
Но по формуле Грина левая часть последнего
неравенства равна криволинейному
интегралу по границе
области
,
который, по предположению, равен нулю.
Следовательно, последнее неравенство
противоречит условию (2), и значит,
предположение, чтоотлично от нуля хотя бы в одной точке,
неверно. Отсюда вытекает, чтово всех точках данной области
,
а следовательно
.
Теорема доказана.
Соседние файлы в папке Высшая математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формула Грина на плоскости
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Ориентация границы плоской области.
Начать изучение
-
Формула Грина.
Начать изучение
-
Формула Грина для многосвязной области.
Начать изучение
-
Применение формулы Грина к вычислению площадей.
Начать изучение
-
Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).
Начать изучение
Ориентация границы плоской области.
Напомним, что областью в (boldsymbol{R}^{2}) называется открытое связное множество, а замыкание области получается присоединением к области ее границы.
Теорема Жордана утверждает, что любая простая (без точек самопересечения) замкнутая кривая разделяет плоскость на две области, ограниченную и неограниченную, общей границей которых она является.
Область (Omega subset boldsymbol{R}^{2}) называется односвязной, если для любого простого контура (gamma subset Omega) ограничиваемая этим контуром область (Omega_{1} subset Omega). В частности, область на рис. 51.1 односвязна.
Будем говорить, что простой контур (Gamma) ориентирован положительно, если при обходе контура ограничиваемая им область остается слева (рис. 51.1). Противоположно ориентированный контур будем обозначать через (Gamma^{-}).
Формула Грина.
Теорема.
Пусть функции (P(x, y)) и (Q(x, y)) непрерывно дифференцируемы в односвязной области (Omega subset boldsymbol{R}^{2}), а простой кусочно гладкий контур (Gamma subset Omega) ограничивает область (G subset Omega). Тогда справедлива формула Грина
$$
intlimits_{partial G} P dx + Q dy = iintlimits_{G} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy,label{ref1}
$$
где (partial G) есть положительно ориентированная граница области (G).
Доказательство.
(circ) Докажем сначала формулу eqref{ref1} в наиболее простом случае, когда область (G) еще и элементарна относительно обеих координатных осей, то есть существуют такие кусочно непрерывно дифференцируемые и непрерывные функции (varphi(x)), (psi(x)), (x in [a, b]), и (alpha(y)), (beta(y)), (y in [c, d]), что (рис. 51.2)
$$
overline{G} = {(x, y): a leq x leq b, varphi(x) leq y leq psi(x)} = {(x, y): c leq y leq d, alpha(x) leq x leq beta(x)}.nonumber
$$
Примерами таких областей являются внутренности круга, эллипса, треугольника.
Применяя формулу сведения двойного интеграла к повторному, получаем равенства
$$
iintlimits_{G} frac{partial P}{partial y} (x, y) dx dy =-intlimits_{a}^{b} dx intlimits_{varphi(x)}^{psi(x)} frac{partial P}{partial y} (x, y) dx dy =\= intlimits_{a}^{b} P(x, varphi(x))dx-intlimits_{a}^{b} P(x, psi(x))dx =\= intlimits_{ABCD} P dx + intlimits_{DE} P dx + intlimits_{EFMN} P dx + intlimits_{NA} P dx = intlimits_{partial G} P dx.label{ref2}
$$
При выводе формулы eqref{ref2} была использована формула для криволинейного интеграла (intlimits_{Gamma} P dx) по кривой (Gamma), являющейся графиком функции. Добавленные интегралы по вертикальным отрезкам (DE) и (NA) равны нулю, так как на этих отрезках (x = operatorname{const}).
Аналогично доказывается формула
$$
iintlimits_{G} frac{partial Q(x, y)}{partial x} dx dy = intlimits_{partial G} Q(x, y) dy.label{ref3}
$$
Складывая равенства eqref{ref2} и eqref{ref3}, получаем формулу Грина eqref{ref1}.
Пусть теперь область (G) по-прежнему ограничена кусочно гладкой замкнутой кривой (partial G). Предположим, что ее можно кусочно гладкой простой кривой (Gamma) (перегородкой) разбить на две области простейшего вида, рассмотренные выше (рис. 51.3). Тогда
$$
partial G_{1} = Gamma cup Gamma_{1}, partial G_{2} = Gamma^{-} cup Gamma_{2}.nonumber
$$
Применяя формулу Грина в каждой из областей (G_{1}) и (G_{2}), получаем
$$
iintlimits_{G_{1}} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy = intlimits_{partial G} P dx + Q dy = intlimits_{Gamma_{1}} P dx + Q dy + intlimits_{Gamma} P dx + Q dy,nonumber
$$
$$
iintlimits_{G_{1}} left[frac{partial Q(x, y)}{partial x}-frac{partial P(x, y)}{partial y}right] dx dy = intlimits_{Gamma_{2}} P dx + Q dy + intlimits_{Gamma^{-}} P dx + Q dy.nonumber
$$
Складывая эти два равенства и учитывая, что криволинейные интегралы по противоположно ориентированным кривым (Gamma) и (Gamma^{-}) взаимно уничтожаются, получаем, что формула Грина eqref{ref1} верна для области (G = G_{1} cup G_{2}).
При помощи математической индукции теперь легко обобщить формулу Грина на односвязную область, которая при помощи (n-1) непересекающихся гладких перегородок разбивается на области (G_{1}, ldots, G_{n}) простейшего вида (рис. 51.3). В частности, формула Грина обобщается на многоугольные области, ограниченные простыми замкнутыми ломаными. В общем случае можно доказать формулу Грина, аппроксимируя область с кусочно гладкой границей многоугольной областью. (bullet)
Формула Грина для многосвязной области.
Формула Грина может быть обобщена и на случай многосвязной ((n)-связной) области, ограниченной внешним контуром (Gamma) и непересекающимися внутренними контурами (gamma_{1}, ldots, gamma_{n-1}). Все контуры предполагаются кусочно гладкими. На рис. 51.4 изображены ограниченные двусвязная и трехсвязная области.
Внешний контур ориентируем так, чтобы при его обходе область оставалась слева. Так ориентированный контур будем обозначать (Gamma). А внутренние контуры ориентируем так, чтобы при их обходе область (G) оставалась справа. Будем писать
$$
partial G = left(bigcup_{i=1}^{n} gamma_{i}^{-}right) bigcup Gamma.nonumber
$$
Пусть непрерывно дифференцируемое поле ((P(x, y), Q(x, y))) задано в двусвязной области (G), ограниченной кусочно гладкими простыми контурами: внешним (Gamma) и внутренним (gamma) (рис. 51.4).
При помощи гладких перегородок (gamma_{3}) и (gamma_{4}) (рис. 51.5) разделим двусвязную область (G) на две односвязных, (G_{1}) и (G_{2}). Как видно из рис. 51.5,
$$
Gamma = Gamma_{1} cup Gamma_{2}, gamma = gamma_{1} cup gamma_{2}.nonumber
$$
Применяя к (G_{1}) и (G_{2}) формулу Грина для односвязной области, получаем (рис. 51.5)
$$
iintlimits_{G_{1}} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G_{1}} P dx + Q dy = left(intlimits_{Gamma_{1}} + intlimits_{gamma_{3}} + intlimits_{gamma_{1}^{-}} + intlimits_{gamma_{4}}right) (P dx + Q dy),nonumber
$$
$$
iintlimits_{G_{2}} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G_{1}} P dx + Q dy = left(intlimits_{Gamma_{2}} + intlimits_{gamma_{4}^{-}} + intlimits_{gamma_{2}^{-}} + intlimits_{gamma_{3}^{-}}right) (P dx + Q dy),nonumber
$$
где в правой части употреблено сокращенное обозначение для суммы четырех криволинейных интегралов по соответствующим кривым. Складывая эти равенства и учитывая, что криволинейные интегралы по противоположно ориентированным кривым взаимно уничтожаются, получаем
$$
iintlimits_{G} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{Gamma} P dx + Q dy + intlimits_{gamma^{-}} P dx + Q dy = intlimits_{partial G} P dx + Q dy.nonumber
$$
Формально формула Грина для двусвязной области имеет тот же вид, что и для односвязной, если (displaystyleintlimits_{partial G} P dx + Q dy) понимать как сумму криволинейных интегралов по (Gamma) и (gamma^{-}).
Индукцией эта формула Грина обобщается и на (n)-связную область:
$$
iintlimits_{G} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = intlimits_{partial G} P dx + Q dy = intlimits_{Gamma} P dx + Q dy + sum_{i=1}^{substack{n-1}} intlimits_{gamma_{i}^{-}} P dx + Q dy.nonumber
$$
Применение формулы Грина к вычислению площадей.
Полагая в формуле Грина eqref{ref1} (Q = x), (P = -y), получаем формулу для вычисления площади, ограниченной гладким контуром,
$$
m(G) = frac{1}{2} intlimits_{partial G} x dy-y dx.label{ref4}
$$
Иногда при практическом применении формулы eqref{ref4} полезно воспользоваться тем, что
$$
x dy-y dx = (x^{2} + y^{2})dleft(operatorname{arctg} frac{y}{x}right).nonumber
$$
Пример 1.
Найти площадь, ограниченную кривой (рис. 51.6)
$$
x = frac{3at}{1 + t^{3}},quad y = frac{3at^{2}}{1 + t^{3}},quad 0 leq t leq +infty.nonumber
$$
Решение.
(vartriangle) Эта кривая (декартов лист), как нетрудно показать, симметрична относительно прямой (y = x).
Поэтому можно ограничиться вычислением площади половинки листа, для которой (0 leq t leq 1). Получаем
$$
x dy-y dx = (x^{2} + y^{2})dleft(operatorname{arctg} frac{y}{x}right) = frac{9a^{2}t^{2}(1 + t^{2})}{(1 + t^{3})^{2}}d(operatorname{arctg} t) = frac{9a^{2}t^{2}}{(1 + t^{3})^{2}}dt = -3a^{2} dleft(frac{1}{1 + t^{3}}right).nonumber
$$
По формуле eqref{ref4} площадь половинки листа Декарта равна
$$
m(G) = frac{1}{2} intlimits_{Gamma} x dy-y dx = -frac{3a^{2}}{2} intlimits_{0}^{1} dleft(frac{1}{1 + t^{3}}right) = frac{3a^{2}}{4},nonumber
$$
а искомая площадь равна (displaystylefrac{3a^{2}}{2}). (blacktriangle)
Условия независимости криволинейного интеграла второго рода от пути интегрирования (плоский случай).
Пусть в области (G subset boldsymbol{R}^{2}) задано непрерывное векторное поле ((P(x, y), Q(x, y))). Например, это может быть силовое поле. Возьмем в области (G) две произвольные точки, (A(x_{0}, y_{0})) и (B(x, y)). Соединим эти две точки кусочно гладкой кривой (Gamma_{AB}), лежащей в (G). Вычислим интеграл (displaystyleintlimits_{Gamma_{AB}} P dx + Q dy). Этот интеграл можно интерпретировать как работу силы при движении точки по кривой (Gamma_{AB}). Вообще говоря, (displaystyleintlimits_{Gamma_{AB}} P dx + Q dy) зависит как от точек (A) и (B), так и от пути, по которому мы из точки (A) приходим в точку (B). Наша цель — выяснить условия независимости величины этого интеграла (работы силы) от пути интегрирования.
Теорема 1.
Следующие три условия эквивалентны:
- для любой замкнутой ломаной (L subset G)
$$
intlimits_{L} P dx + Q dy = 0;label{ref5}
$$ - (displaystyleintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB} subset G), соединяющей точки (A) и (B);
- поле ((P(x, y), Q(x, y))) потенциально, то есть существует такая непрерывно дифференцируемая функция (U(x, y)) (потенциал поля), что
$$
P(x, y) dx + Q(x, y) dy = dU,nonumber
$$
$$
P(x, y) = frac{partial U(x, y)}{partial x},quad Q(x, y) = frac{partial U(x, y)}{partial y}.nonumber
$$
Доказательство.
(circ) Доказательство проведем по круговой схеме: (1.Rightarrow 2. Rightarrow 3.Rightarrow 1.)
- Докажем, что (1. Rightarrow 2.) Пусть выполнено условие (1.) Возьмем две произвольных точки, (A) и (B), в области (G). Соединим их ломаной (L_{AB}). Пусть (L’_{AB}) — любая другая ломаная, соединяющая точки (A) и (B). Тогда (L = L_{AB} + L’_{BA}) есть замкнутая ломаная. В силу условия (1.) имеем
$$
0 = intlimits_{L} P dx + Q dy = intlimits_{L_{AB}} P dx + Q dy + intlimits_{L’_{BA}} P dx + Q dy =\= intlimits_{L_{AB}} P dx + Q dy-intlimits_{L’_{BA}} P dx + Q dy,nonumber
$$
$$
intlimits_{L_{AB}} P dx + Q dy = intlimits_{L’_{BA}} P dx + Q dy,nonumber
$$
то есть интеграл (nonumberintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB}), соединяющей точки (A) и (B). - Докажем, что (2. Rightarrow 3.) Пусть (displaystyleintlimits_{L_{AB}} P dx + Q dy) не зависит от ломаной (L_{AB}), соединяющей точки (A) и (B). Фиксируем точку (A(x_{0}, y_{0})), а точку (B(x, y)) будем считать переменной. Тогда (displaystyleintlimits_{L_{AB}} P dx + Q dy) зависит только от точки (B), и, следовательно, в области (G) определена функция
$$
U(x, y) = intlimits_{L_{AB}} P dx + Q dy.nonumber
$$
Покажем, что функция (U(x, y)) — потенциал поля. Соединим точки (B(x, y)) и (C(x + Delta x, y)) отрезком (BC), лежащим в области (G) (рис. 51.7). Это всегда можно сделать при достаточно малом (Delta x), так как (G) — открытое множество. Тогда
$$
frac{1}{Delta x} (u(x + Delta x, y)-U(x, y)) = frac{1}{Delta x} left[intlimits_{L_{ABC}} P dx + Q dy-intlimits_{L_{AB}} P dx + Q dyright] =\= frac{1}{Delta x} intlimits_{BC} P dx + Q dy = frac{1}{Delta x} intlimits_{x}^{x + Delta x} P(xi, y) dxi.nonumber
$$
Рис. 51.7 Применяя при фиксированном (y) к непрерывной функции (P(xi, y)) интегральную теорему о среднем, получаем
$$
frac{1}{Delta x} (U(x + Delta x, y)-U(x, y)) = P(x + theta Delta x, y), mbox{где} 0 < theta < 1.nonumber
$$Воспользовавшись непрерывностью функции (P(x, y)) и переходя к пределу при (Delta x rightarrow 0), получаем
$$
lim_{Delta x rightarrow 0} frac{U(x + Delta x, y)-U(x, y)}{Delta x} = P(x, y) = frac{partial U}{partial x}.nonumber
$$Аналогично доказывается, что (displaystylefrac{partial U}{partial y} = Q(x, y)).
Так как (P(x, y)) и (Q(x, y)) — непрерывные в области (G) функции, то функция (U(x, y)) непрерывно дифференцируема в области (G).
- Докажем, что (3. Rightarrow 1.) Это следует из более общего утверждения: если (P(x, y) dx + Q(x, y) dy = dU), то для любого кусочно гладкого контура (gamma) справедливо равенство (displaystyleintlimits_{gamma} P dx + Q dy = 0). Действительно, если (x = x(t), y = y(t), alpha leq t leq beta), есть уравнение кривой (gamma), то
$$
intlimits_{gamma} P dx + Q dy = intlimits_{alpha}^{beta} [P(x(t), y(t))x'(t) + Q(x(t), y(t))y'(t)] dt =\= intlimits_{alpha}^{beta} left[frac{partial U}{partial x} (x(t), y(t))x'(t) + frac{partial U}{partial y} Q(x(t), y(t))y'(t)right] dt =\= intlimits_{alpha}^{beta} frac{d}{dt} [U(x(t), y(t))] dt = U(x(beta), y(beta))-U(x(alpha), y(alpha)) = 0,nonumber
$$
так как начало и конец замкнутой кривой совпадают. (bullet)
Следствие.
Если (displaystyleintlimits_{gamma} P dx + Q dy) равен нулю по любой замкнутой ломаной, то этот интеграл равен нулю и по любому кусочно гладкому контуру (gamma).
(circ) Пусть (displaystyleintlimits_{L} P dx + Q dy = 0) для любой замкнутой ломаной (L). Тогда существует потенциал (U(x, y)) и
$$
P dx + Q dy = frac{partial U}{partial x} (x, y) dx + frac{partial U}{partial y} (x, y) dy.nonumber
$$
Следовательно, (displaystyleintlimits_{gamma} P dx + Q dy = 0). (bullet)
Теорема 1 не дает практического способа для выяснения вопроса о потенциальности поля (P, Q). Для односвязной области (G) докажем эффективный критерий, основанный на использовании формулы Грина.
Теорема 2.
Для того чтобы дифференцируемое в области (G) поле было потенциальным, необходимо, а в случае односвязной области и достаточно, чтобы выполнялось условие
$$
frac{partial P(x, y)}{partial y} = frac{partial Q(x, y)}{partial x}.label{ref6}
$$
Доказательство.
(circ) Необходимость. Пусть поле ((P(x, y), Q(x, y))) непрерывно дифференцируемо и потенциально. Тогда
$$
P(x, y) = frac{partial U(x, y)}{partial x},quad Q(x, y) = frac{partial U(x, y)}{partial y},nonumber
$$
откуда
$$
frac{partial Q(x, y)}{partial x} = frac{partial^{2} U(x, y)}{partial x partial y},quad frac{partial P(x, y)}{partial y} = frac{partial^{2} U(x, y)}{partial y partial x}.nonumber
$$
Так как производные (partial P/partial y) и (partial Q/partial x) непрерывны, то смешанные производные (U_{xy}), (U_{yx}) также непрерывны, а следовательно, равны. Условие eqref{ref6} выполнено в области (G).
Достаточность. Пусть поле (P, Q) задано в односвязной области (G subset boldsymbol{R}^{2}) и выполнено условие eqref{ref6}.
Возьмем произвольную простую замкнутую ломаную (L subset G). Так как область (G) односвязна, то ограничиваемая ломаной (L) область (Omega subset G) и к ней применима формула Грина
$$
intlimits_{L} P dx + Q dy = intlimits_{Omega} left(frac{partial Q}{partial x}-frac{partial P}{partial y}right) dx dy = 0.label{ref7}
$$
Таким образом, интеграл eqref{ref7} равен нулю для любой простой замкнутой ломаной (L).
Теперь нетрудно показать, что интеграл eqref{ref7} равен нулю для любой замкнутой ломаной (даже имеющей точки самопересечения).
Для трехзвенной ломаной интеграл eqref{ref7} всегда равен нулю, если эта ломаная замкнута. Если три ее вершины не лежат на одной прямой, то трехзвенная ломаная будет простой и по доказанному интеграл eqref{ref7} равен нулю. Если же все три вершины лежат на одной прямой, то и в этом случае, как легко видеть, интеграл равен нулю (рис. 51.8).
То, что интеграл eqref{ref7} равен нулю для любой (n)-звенной замкнутой ломаной, докажем индукцией по числу звеньев ломаной.
Пусть выполнено условие eqref{ref6} и интеграл eqref{ref7} равен нулю по любой замкнутой ломаной, число звеньев которой меньше, чем (n). Покажем тогда, что криволинейный интеграл eqref{ref7} равен нулю и по любой замкнутой (n)-звенной ломаной. Если ломаная (L(A_{1}, A_{2}, ldots, A_{n}, A_{1})) простая, то это уже доказано. Пусть у (L) есть точки самопересечения. Предположим, что два звена, (A_{1}A_{2}) и (A_{k}A_{k + 1}), пересекаются. Тогда либо они пересекаются в единственной точке В (рис. 51.8), либо эти два звена пересекаются по целому отрезку. В этом случае точки (A_{1}), (A_{2}), (A_{k}), (A_{k + 1}) лежат на одной прямой (рис. 51.9).
Рассмотрим первый случай. За последующими рассуждениями проще следить по рис. 51.9. В случаях а) и б) ломаная (L) будет объединением замкнутых ломаных (L_{1}(B, A_{k + 1}, ldots, A_{n}, A_{1}, B)) и (L_{2}(B, A_{2}, ldots, A_{k}, B)). Количество звеньев (L_{1}) и (L_{2}) меньше (n). По предположению индукции интеграл eqref{ref7} по каждой из этих ломаных равен нулю. Следовательно, он равен нулю и по их объединению — ломаной (L).
Аналогично рассматривается и второй случай, когда точки (A_{1}), (A_{2}), (A_{k}), (A_{k + 1}) лежат на одной прямой и отрезки (A_{1}A_{2}) и (A_{k}A_{k + 1}) пересекаются. Без ограничения общности можно считать, что точка (A_{k}) лежит на отрезке (A_{1}A_{2}). Тогда (L) есть объединение замкнутых ломаных (L_{1}(A_{k}, A_{k + 1}, ldots, A_{n}, A_{1}, A_{k})) и (L_{2}(A_{k}, A_{2}, ldots, A_{k-1}, A_{k})), имеющих меньше, чем (n) звеньев. Интеграл eqref{ref7} по (L_{1}) и (L_{2}) равен нулю. Следовательно, он равен нулю и по ломаной (L).
Так как интеграл eqref{ref7} равен нулю по любой замкнутой ломаной (L subset G), то в силу теоремы 1 поле ((P, Q)) будет потенциальным. (bullet)
Заметим, что условие односвязности области существенно для справедливости теоремы 2. Подтвердим это следующим примером.
Пример 2.
Показать, что непрерывно дифференцируемое при (x^{2} + y^{2} > 0) плоское векторное поле
$$
P(x, y) = -frac{omega}{2pi} frac{y}{x^{2} + y^{2}},quad Q(x, y) = frac{omega}{2pi} frac{x}{x^{2} + y^{2}}label{ref8}
$$
удовлетворяет условию eqref{ref6}, но не является потенциальным при (omega neq 0).
Решение.
(vartriangle) Условие eqref{ref6} выполняется, так как
$$
frac{partial P}{partial y} = frac{omega}{2pi} frac{y^{2}-x^{2}}{(y^{2} + x^{2})^{2}} = frac{partial Q}{partial x}.nonumber
$$
Рассмотрим окружность (C_{R}), заданную уравнениями (x = R cos t), (y = R sin t), (0 leq t leq 2pi). Тогда
$$
intlimits_{C_{R}} P dx + Q dy = frac{omega}{2pi} intlimits_{C_{R}} frac{x dy-y dx}{x^{2} + y^{2}} = frac{omega}{2pi} intlimits_{0}^{2pi} dt = omeganonumber
$$
и в силу теоремы 1 поле ((P, Q)) не может быть потенциальным.
Теорема 2 неприменима, поскольку поле определено в неодносвязной области (G = {(x, y): x^{2} + y^{2} > 0}). (blacktriangle)
Замечание
В гидродинамике поле eqref{ref8} интерпретируется как поле скоростей точечного вихря, расположенного в точке ((0, 0)) и имеющего интенсивность (omega). Если перейти к полярным координатам (r), (varphi), то
$$
v = (p, Q) = frac{omega}{2pi r} (-sin varphi, cos varphi).nonumber
$$
Жидкие частицы вращаются по концентрическим окружностям с постоянными скоростями, обратно пропорциональными расстоянию от точечного вихря (рис. 51.10).
From Wikipedia, the free encyclopedia
This article is about the theorem in the plane relating double integrals and line integrals. For Green’s theorems relating volume integrals involving the Laplacian to surface integrals, see Green’s identities.
Not to be confused with Green’s law for waves approaching a shoreline.
In vector calculus, Green’s theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes’ theorem.
Theorem[edit]
Let C be a positively oriented, piecewise smooth, simple closed curve in a plane, and let D be the region bounded by C. If L and M are functions of (x, y) defined on an open region containing D and have continuous partial derivatives there, then
where the path of integration along C is anticlockwise.[1][2]
In physics, Green’s theorem finds many applications. One is solving two-dimensional flow integrals, stating that the sum of fluid outflowing from a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green’s theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter.
Proof when D is a simple region[edit]
If D is a simple type of region with its boundary consisting of the curves C1, C2, C3, C4, half of Green’s theorem can be demonstrated.
The following is a proof of half of the theorem for the simplified area D, a type I region where C1 and C3 are curves connected by vertical lines (possibly of zero length). A similar proof exists for the other half of the theorem when D is a type II region where C2 and C4 are curves connected by horizontal lines (again, possibly of zero length). Putting these two parts together, the theorem is thus proven for regions of type III (defined as regions which are both type I and type II). The general case can then be deduced from this special case by decomposing D into a set of type III regions.
If it can be shown that
-
(1)
and
-
(2)
are true, then Green’s theorem follows immediately for the region D. We can prove (1) easily for regions of type I, and (2) for regions of type II. Green’s theorem then follows for regions of type III.
Assume region D is a type I region and can thus be characterized, as pictured on the right, by
where g1 and g2 are continuous functions on [a, b]. Compute the double integral in (1):
-
(3)
Now compute the line integral in (1). C can be rewritten as the union of four curves: C1, C2, C3, C4.
With C1, use the parametric equations: x = x, y = g1(x), a ≤ x ≤ b. Then
With C3, use the parametric equations: x = x, y = g2(x), a ≤ x ≤ b. Then
The integral over C3 is negated because it goes in the negative direction from b to a, as C is oriented positively (anticlockwise). On C2 and C4, x remains constant, meaning
Therefore,
-
(4)
Combining (3) with (4), we get (1) for regions of type I. A similar treatment yields (2) for regions of type II. Putting the two together, we get the result for regions of type III.
Proof for rectifiable Jordan curves[edit]
We are going to prove the following
We need the following lemmas whose proofs can be found in:[3]
Lemma 1 (Decomposition Lemma) — Assume 







- Each one of the subregions contained in
, say
, is a square from
.
- Each one of the remaining subregions, say
, has as boundary a rectifiable Jordan curve formed by a finite number of arcs of
and parts of the sides of some square from
.
- Each one of the border regions
can be enclosed in a square of edge-length
.
- If
is the positively oriented boundary curve of
, then
- The number
of border regions is no greater than
, where
is the length of
.
Lemma 2 — Let 




Lemma 3 — Let 


and
where 


Now we are in position to prove the theorem:
Proof of Theorem. Let 










Put 
For each 

Every point of a border region is at a distance no greater than 




This yields
We may as well choose 

The remark in the beginning of this proof implies that the oscillations of 


By Lemma 1(iii),
Combining these, we finally get
for some 

Validity under different hypotheses[edit]
The hypothesis of the last theorem are not the only ones under which Green’s formula is true. Another common set of conditions is the following:
The functions 






As a corollary of this, we get the Cauchy Integral Theorem for rectifiable Jordan curves:
Theorem (Cauchy) — If 



the integral being a complex contour integral.
Proof
We regard the complex plane as 





Now, analyzing the sums used to define the complex contour integral in question, it is easy to realize that
the integrals on the RHS being usual line integrals. These remarks allow us to apply Green’s Theorem to each one of these line integrals, finishing the proof.
Multiply-connected regions[edit]
Theorem. Let 

where 

Suppose 


is Riemann-integrable over 
Relationship to Stokes’ theorem[edit]
Green’s theorem is a special case of the Kelvin–Stokes theorem, when applied to a region in the 
We can augment the two-dimensional field into a three-dimensional field with a z component that is always 0. Write F for the vector-valued function 
The Kelvin–Stokes theorem:
The surface 


The expression inside the integral becomes
Thus we get the right side of Green’s theorem
Green’s theorem is also a straightforward result of the general Stokes’ theorem using differential forms and exterior derivatives:
Relationship to the divergence theorem[edit]
Considering only two-dimensional vector fields, Green’s theorem is equivalent to the two-dimensional version of the divergence theorem:
where 


To see this, consider the unit normal 




Start with the left side of Green’s theorem:
Applying the two-dimensional divergence theorem with 
Area calculation[edit]
Green’s theorem can be used to compute area by line integral.[4] The area of a planar region 
Choose 


Possible formulas for the area of 
History[edit]
It is named after George Green, who stated a similar result in an 1828 paper titled An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism. In 1846, Augustin-Louis Cauchy published a paper stating Green’s theorem as the penultimate sentence. This is in fact the first printed version of Green’s theorem in the form appearing in modern textbooks. Bernhard Riemann gave the first proof of Green’s theorem in his doctoral dissertation on the theory of functions of a complex variable.[5][6]
See also[edit]
- Planimeter – Tool for measuring area.
- Method of image charges – A method used in electrostatics that takes advantage of the uniqueness theorem (derived from Green’s theorem)
- Shoelace formula – A special case of Green’s theorem for simple polygons
References[edit]
- ^ Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). Mathematical Methods for Physics and Engineering. Cambridge University Press. ISBN 978-0-521-86153-3.
- ^ Spiegel, M. R.; Lipschutz, S.; Spellman, D. (2009). Vector Analysis. Schaum’s Outlines (2nd ed.). McGraw Hill. ISBN 978-0-07-161545-7.
- ^ Apostol, Tom (1960). Mathematical Analysis (1 ed.). Reading, Massachusetts, U.S.A.: Addison-Wesley Publishing Company, INC.
- ^ a b Stewart, James (1999). Calculus (6th ed.). Thomson, Brooks/Cole. ISBN 9780534359492.
- ^ George Green, An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism (Nottingham, England: T. Wheelhouse, 1828). Green did not actually derive the form of «Green’s theorem» which appears in this article; rather, he derived a form of the «divergence theorem», which appears on pages 10–12 of his Essay.
In 1846, the form of «Green’s theorem» which appears in this article was first published, without proof, in an article by Augustin Cauchy: A. Cauchy (1846) «Sur les intégrales qui s’étendent à tous les points d’une courbe fermée» (On integrals that extend over all of the points of a closed curve), Comptes rendus, 23: 251–255. (The equation appears at the bottom of page 254, where (S) denotes the line integral of a function k along the curve s that encloses the area S.)
A proof of the theorem was finally provided in 1851 by Bernhard Riemann in his inaugural dissertation: Bernhard Riemann (1851) Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse (Basis for a general theory of functions of a variable complex quantity), (Göttingen, (Germany): Adalbert Rente, 1867); see pages 8–9. - ^ Katz, Victor (2009). «22.3.3: Complex Functions and Line Integrals». A History of Mathematics: An Introduction. Addison-Wesley. pp. 801–5. ISBN 978-0-321-38700-4.
Further reading[edit]
- Marsden, Jerrold E.; Tromba, Anthony J. (2003). «The Integral Theorems of Vector Analysis». Vector Calculus (Fifth ed.). New York: Freeman. pp. 518–608. ISBN 0-7167-4992-0.
External links[edit]
- Green’s Theorem on MathWorld



















![intlimits_V (varphi nabla^2 psi - psi nabla^2 varphi),d^3x = ointlimits_S left[varphi frac{partial psi}{partial n} - psi frac{partial varphi}{partial n}right] ,da](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2fb51522a69aabe631d19426dce0202722a8000)

![ointlimits_{partial U} left[ {1 over |mathbf{x} - mathbf{y}|} {partial phi over partial n} (mathbf{y}) - phi(mathbf{y}) {partial over partial n_mathbf{y}} {1 over |mathbf{x} - mathbf{y}|}right], dS_mathbf{y} - intlimits_U left[ {1 over |mathbf{x} - mathbf{y}|} nabla^2 phi(mathbf{y})right], dV_mathbf{y} = k](https://wikimedia.org/api/rest_v1/media/math/render/svg/33bd3208ad67069ea3817b7ecd9e6519379cac07)


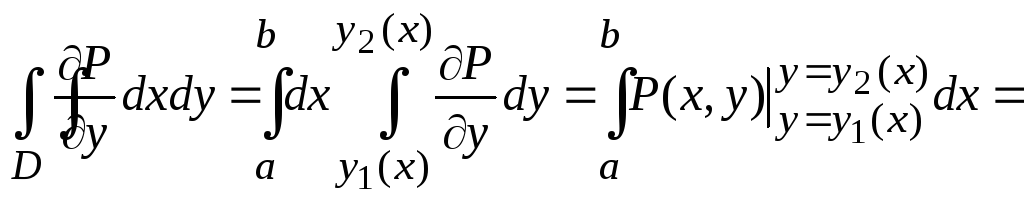






![{displaystyle {begin{aligned}iint _{D}{frac {partial L}{partial y}},dA&=int _{a}^{b},int _{g_{1}(x)}^{g_{2}(x)}{frac {partial L}{partial y}}(x,y),dy,dx\&=int _{a}^{b}left[L(x,g_{2}(x))-L(x,g_{1}(x))right],dx.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9031079d3891809000938ae68b63ab7a382f897f)

























![{displaystyle {begin{aligned}&int _{Gamma _{0}}p(x,y),dx+q(x,y),dy-sum _{i=1}^{n}int _{Gamma _{i}}p(x,y),dx+q(x,y),dy\[5pt]={}&int _{D}left{{frac {partial q}{partial e_{1}}}(x,y)-{frac {partial p}{partial e_{2}}}(x,y)right},d(x,y).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0a3feffd38b2ac095b5e5f36bedf83d12872aff)


![{displaystyle nabla times mathbf {F} cdot mathbf {hat {n}} =left[left({frac {partial 0}{partial y}}-{frac {partial M}{partial z}}right)mathbf {i} +left({frac {partial L}{partial z}}-{frac {partial 0}{partial x}}right)mathbf {j} +left({frac {partial M}{partial x}}-{frac {partial L}{partial y}}right)mathbf {k} right]cdot mathbf {k} =left({frac {partial M}{partial x}}-{frac {partial L}{partial y}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a90d83bc979c291f726a35cf8811cbf7706540)









