Краткий конспект аксиома параллельных прямых
Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.
Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).
Аксиома параллельности:
Через точку, не лежащую на данной прямой, на плоскости можно провести только одну прямую , параллельную данной прямой.
Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.
Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
Свойства и признаки параллельных прямых

- Две прямые, параллельные третьей, параллельны.
- Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
- Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
- Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,
Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.
Это конспект по теме «Параллельные прямые». Выберите дальнейшие действия:
Геометрия. 7 класс
Конспект урока
Аксиома параллельных прямых
Перечень рассматриваемых вопросов:
- Аксиомы и теоремы.
- Исторические сведения об аксиоматическом построении евклидовой геометрии.
- Параллельные и перпендикулярные прямые.
- Признаки параллельности прямых.
- Решение задач на доказательство параллельности прямых.
Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые, параллельны третьей прямой, то они параллельны.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения
Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.
Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.
Аксиома – происходит от греческого «аксиос», что означает «ценный, достойный». Изначально имело смысл «самоочевидная истина».
Теорема – греческое слово, означает «зрелище, представление». В математике греков употреблялось в смысле «истина, доступная созерцанию».
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые параллельны третьей прямой, то они параллельны.
Впервые аксиоматический подход к изложению геометрии был изложен в знаменитом сочинении Евклида «Начала» в III веке до нашей эры. Геометрию, которую мы изучаем, по сей день, называют евклидовой. Схема изучения геометрии представлена так: задаются начальные понятия (точка, прямая, плоскость), определения фигур (отрезок, луч, треугольник и др.). Затем изучаются свойства или отношения между ними в виде аксиом или теорем.
Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.
- Через любые две точки проходит прямая, и притом только одна.
- На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
Евклид является автором аксиоматического подхода к построению геометрии.
Аксиома параллельных прямых:
через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
На рисунке через точку М проведены две прямые. Но только одна из них прямая b параллельна прямой а.
Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.
Следствия из аксиомы параллельных прямых.
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство методом от противного.
Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.
2. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство методом от противного.
Пусть a ║ c, b ║ c.
Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.
Разбор заданий тренировочного модуля
№ 1. Доказать существование прямой, параллельной данной.
- Проведём через точку М прямую c ┴ а.
- Затем проведём прямую b ┴ c.
- Так как прямые a и b перпендикулярны прямой c, то они параллельны.
№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.
Сколько из них пересекает прямую р?
1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.
2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.
Что такое аксиома, теорема и доказательство теоремы
О чем эта статья:
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
- Через любые две точки проходит единственная прямая.
- Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки. А точки из одной части лежат по одну сторону от данной точки.
- На любом луче от его начала можно отложить только один отрезок, равный данному.
- Отрезки, полученные сложением или вычитанием соответственно равных отрезков — равны.
- Каждая прямая на плоскости разбивает эту плоскость на две полуплоскости. При этом если две точки принадлежат разным частям, то отрезок, который соединяет эти две точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок, соединяющий эти точки, не пересекается с прямой.
- От любого луча на плоскости в заданную сторону можно отложить только один угол, который равен данному. Все развернутые углы равны.
- Углы равны, если они получились путем сложения или вычитания соответственно равных углов.
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
- если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
- если две прямые параллельны третьей прямой, то они параллельны.
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
- Синтетический или синтез — метод, при котором данное предложение выступает, как необходимое следствие другого, уже доказанного.
- Аналитический или анализ — обратный синтезу способ. Рассуждения всегда начинаются с доказываемой теоремы и закачиваются другой известной истиной.
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
- Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.
- Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
- Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
- прямая теорема: в треугольнике против равных сторон лежат равные углы.
- обратная теорема: в треугольнике против равных углов лежат равные стороны.
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
- Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
- Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
- Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
- Обратная противоположной: если прямые не параллельны, соответственные углы не равны.
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол, противолежащий стороне а.
Следствия из теоремы косинусов:
- при b² + c² – a² > 0 угол α будет острым;
- при b² + c² – a² = 0 угол α будет прямым, что соответствуем теореме Пифагора;
- при b² + c² – a²
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
источники:
http://resh.edu.ru/subject/lesson/7300/conspect/
http://skysmart.ru/articles/mathematic/aksioma-teorema
«Параллельные прямые»
Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.
Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).
Аксиома параллельности:
Через точку, не лежащую на данной прямой, на плоскости можно провести только одну прямую, параллельную данной прямой.
Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.
Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
Свойства и признаки параллельных прямых:
- Две прямые, параллельные третьей, параллельны.
- Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.
- Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
- Если две параллельные прямые пересечены секущей, то:
– сумма внутренних односторонних углов равна 180°,
– накрест лежащие углы равны,
– соответственные углы равны,
Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.
Это конспект по теме о параллельных прямых. Выберите дальнейшие действия:
- Перейти к следующему конспекту: ЗАДАЧИ по теме Параллельные прямые
- Вернуться к Списку конспектов по геометрии
Математическая система, приписываемая Евклиду 
Евклидова геометрия — это математическая система, приписываемая Александрию греческому математику Евклиду, которуюон описал в своем учебнике по геометрии : Элементы. Метод Евклида состоит в допущении небольшого набора интуитивно привлекательных аксиом и вывод из них многих других утвержденных (теорем ). Хотя многие из результатов Евклида были заявлены более ранними математиками, Евклид был первым, кто показал, как эти предложения могут вписаться в всеобъемлющую дедуктивную и логическую систему. Элементы начинаются с геометрии плоскости,которая до сих пор преподается в средней школе (старшая школа) как первая аксиоматическая система и первые примеры формального доказательства. Он переходит к твердотельной геометрии из трех измерений. Большая часть Элементов констатирует результаты того, что сейчас называется алгеброй и теорией чисел, объясненных на геометрическом языке.
Более двух тысяч лет прилагать «евклидово» «не было необходимости, потому что никакой другойвидрии не был придуман. Аксиомы Евклида казались интуитивно очевидными (за возможное исключение параллельного постулата ), что Сегодня, известно множество других самосогласованных неевклидовых геометрий, первые из которых были обнаружены в начале 19 века. 237>теории общей теории относительности Альберта Эйнштейна, что физическое пространство само по себе не евклидовым, а евклидово пространство является хорошим приближением только в краткосрочнойперспективе (относительно силы гравитационного поля ).
Евклидова геометрия примером синтетической геометрии, поскольку она логически вытекает из аксиом, определяющие основные свойства геометрических объекто в, как точки и линии, предложения об этих объектах, и все это без использования координат для определения этих объектов. В этом отличии от аналитичес кой геометрии, которая использует координаты для геометрических утверждений в алгебраических формулах.
Содержание
- 1 Элементы
- 1.1 Аксиомы
- 1.2 Параллельный постулат
- 2 Методы
- 3 Система измерения и арифметика
- 4 Обозначения и терминология
- 4.1 Названия точек и цифры
- 4.2 Дополнительные и дополнительные углы
- 4.3 Современные версии нотации Евклида
- 5 сомнительные или хорошо известные результаты
- 5.1 Pons Asinorum
- 5.2 Конгруэнтность треугольников
- 5.3 Сумма углового треугольника
- 5.4 Теорема Пифагора
- 5.5 Теорема Фалеса
- 5.6Масштабирование площади и объем
- 6 Приложения
- 7 Как описание структуры пространства
- 8 Более поздние работы
- 8.1 Архимед и Аполлоний
- 8.2 17 век: Декарт
- 8.3 XVIII век
- 8.4 XIX век и другие -Евклидова геометрия
- 8.5 ХХ век и теория относительности
- 9 Учет бесконечности
- 9.1 Бесконечные объекты
- 9.2 Бесконечные процессы
- 10 Логическая основа
- 10.1 Классическая логика
- 10.2 Современные стандарты строгости
- 10.3 Аксиоматические формулировки
- 11 См. Также
- 11.1 Классические теоремы
- 12 Примечания
- 13 Ссылки
- 14 Ранние ссылки
Элементы
Элементы — это в основном систематизация ранее полученных знаний по геометрии. Улучшение по сравнению с более ранними методами лечения было быстро признано, в результате чего было малоса к сохранению более ранних методов.
В Элементах 13 книг:
В книгах I — IV и VI обсуждается геометрия плоскости. Доказано результатов о плоских фигурах, например: «Влюбом треугольнике два угла меньше взятые вместе любым способом, двух прямых». (Книга 1, предложение 17) и теорема Пифагора «В прямоугольных треугольниках квадрат на стороне, ведущей образ прямой угол, равенство квадратам на сторонах, двойной прямой угол». (Книга I, предложение 47)
Книги V и VII — X имеют дело с теорией чисел, где числа рассматривают геометрически как отрезки линии или области. Введены такие понятия, как простые числа и рациональные ииррациональные числа. Доказано, что простых чисел бесконечно много.
Книги XI — XIII касаются твердой геометрии. Типичный результат — это соотношение 1: 3 между объемом конуса и цилиндра с одинаковой высотой и основанием. Платоновы тела построены.
Аксиомы

Евклидова геометрия — это аксиоматическая система, в которой все теоремы («истинные утверждения») выводятся из небольшого числа простых аксиом. До появления неевклидовой геометрии эти аксиомы считались очевидными в физическом мире, так что все теоремы были одинаково верными. Однако рассуждения Евклида от предположений заключению в силе независимо от их физической реальности.
Ближе к началукниги Элементов Евклид дает пять постулатов (аксиом) для плоской геометрии, заявлено в терминах конструкций (как переведено Томасом Хитом):
- Позвольте постулировать следующее:
- Провести прямую линию из любой точки в любую точку.
- Для построения (удлинения) конечной прямой непрерывно по.
- Для описания окружности с любым центром и расстоянием (радиусом).
- Все прямые углы равны друг другу.
- [параллельныйпостулат ]: То есть, если прямая линия падает на два Прямые линии делают внутренние углы на той и той же стороне меньше двух прямых углов, две прямые линии, если они построены бесконечно, пересекаются на той стороне, на которой углы меньше двух прямых углов.
Хотя Евклид только явно утверждает существование из минусов спроектированные объекты, в его рассуждениях неявно, что они уникальны.
Элементы включают в себя следующие пять «общих понятий»:
- Вещи, которые равны одному иже, также равны друг другу (Переходное свойство <6 элемент>Евклидово отношение ).
- равные вычитания из равных, равные равны (свойство равенства вычитания).
- Вещи совпадают друг с другом, равны друг другу (рефлексивное свойство).
- Целое больше, чем часть
Современные науки соглашаются, что постулаты Евклида не обеспечивают полной логической основы, который Евклидовал для своего выступления.>Использовать более обширные и полные наборы аксиом.
Параллельный постулат
Для древних параллельный Найдите такое Доказательство, которое невозможно построить непротиворечивые системы геометрии, как можно построить непротиворечивые системы геометрии, в качестве альтернативы другим аксиомам.. Сам вклид, по-видимому, считал его качественно отличным от других, о чем доказывает эта организация компонентов: его первые 28 утверждений — это те, можно доказать без.
Можно указать альтернативных аксиом, которые логически эквивалентны параллельному постулату (в контексте других аксиом). Например, аксиома Playfair утверждает:
- В плоскости через точку не на заданной прямой может быть проведена не более одной линии, которая никогда не пересекает линию линии.
Предложение «не больше» — это все, что необходимо, поскольку с помощью остальных аксиом можно доказать, что существует хотя бы одна параллельная линия.

Методы доказательства
Евклидова геометрия конструктивна. Постулаты 1, 2, 3 и 5 утверждают существование и уникальность определенных геометрических фигур, и эти утверждения носят конструктивный характер: то есть нам не только говорят,что современные вещи существуют, но также дают методы их создания с помощью не более чем циркуля и линейки без маркировки. В этом смысле геометрия более конкретна, чем многие современные аксиоматические системы, такие как теория множеств, которые часто утверждают существование объектов, не говоря об их построении, или даже утверждают существование объектов, которые не могут быть построены. в рамках теории. Строго говоря, линии на бумаге — это модели объектов,определенных в формальной системе, а не экземпляры этих объектов. Например, евклидова прямая линия не имеет ширины, но любая настоящая нарисованная линия будет. Хотя почти все современные математики считают неконструктивные методы столь же надежными, как и конструктивные, конструктивные доказательства Евклида часто вытесняли ошибочные неконструктивные доказательства — например, некоторые пифагорейские доказательства, которые включают иррациональные числа, которые обычно требуют такогоутверждения, как «как утверждение, как« как утверждение, как «Найдите наивысшую общую меру…»
Евклид часто использует доказательство от противного. Евклидова геометрия также допускает метод наложения, при котором фигура переносится в другую точку пространства. Например, предложение I.4, конгруэнтность одного треугольника сторона-угол-сторона, доказано перемещение из двух треугольников так, чтобы одна из егоадала с равной стороной другого треугольника.. Некоторые современныеметоды лечения использовать шестой постулат, жесткость треугольника, который можно использовать как альтернативу суперпозиции.
Система измерения и арифметика
Евклидова геометрия имеет два основных типа измерений: угол и расстояние. Угловая шкала является абсолютной, и Евклид использует прямой угол в качестве своей основной единицы, так что, например, угол 45- градусов будет называться половиной прямого угла.. Шкала расстояний относительна; одинраз выбирает отрезок с ненулевой в качестве единицы. Добавление одной линейной сегментной модели на конец другого линейного сегмента для увеличения его длины, и аналогично для вычитания.
Измерения площади и объема производятся на основе расстояний. Например, прямоугольник шириной 3 и длиной 4 имеет, представляющую картину, 12. Эта геометрическая интерпретация умножения ограничена методом прямого измерения произведений четырех или более чисел., в доказательствекниги IX, предложение 20.

Евклид называет пару линий, пару плоских или твердых фигур «равными» (ἴσος), если их длина, площадь илиобъем равны соответственно, и аналогично для углов. Более сильный термин «конгруэнтный » относится к идее, что вся фигура имеет тот же размер и форму, что и другая фигура. В качестве альтернативы, две фигуры являются конгруэнтными, если одну можно заменить другим, чтобы она точно совпала с ней. (Переворачивание разрешено.) Таким образом, например, прямоугольник 2×6 и прямоугольник 3×4 равны, но не конгруэнтны, а буква R конгруэнтна своему зеркальному отображению. Фигуры, которые были бысовпадающими, за исключением различных размеров, называются похожими. Соответствующие углы в паре схожих форм конгруэнтны, а соответствующие стороны пропорциональны друг другу.
Обозначения и терминология
Обозначение точек и цифр
Точки обычно называются заглавными буквами алфавита. Другие фигуры как линии, треугольники или круги, именуются указанными точками, чтобы однозначно указать их из формы, например, треугольник ABC обычно представляетсобой треугольник с вершинами в точках A, B C.
Дополнительные и дополнительные углы
Углы, суммы которых прямым углом, называются дополнительными. Дополнительные углы образуются, когда луч имеет одну и ту же вершину и направлен в направлении, которые находятся между двумя исходными лучами, которые образуют прямой угол. Число лучей между двумя исходными лучами бесконечно.
Углы, сумма которых является прямым углом, являются дополнительными.Дополнительные углы образуются, когда луч имеет одну и ту же вершину и направлен в направлении, которые находятся между двумя исходными лучами, которые находятся между двумя исходными лучами, которые образуют прямой угол (угол образного образа 180 градусов). Число лучей между двумя исходными лучами бесконечно.
Современные версии нотации Евклида
В современной терминологии углы обычно измеряются в градусах или радианах.
Современные школьные учебники частоопределяют отдельные цифры, называемые прямые (бесконечные), лучи (полубесконечные) и отрезки линий (конечной длины). Евклид, вместо того, чтобы обсудить луч как объект, который простирается до бесконечности в одном направлении, обычно использовал бы такие выражения, как «если бы линия удлинялась до достаточной длины», хотя он иногда включает «бесконечные линии». «Линия» у Евклида могла быть как прямой, так и изогнутой, при необходимости он использовал более конкретныйтермин «прямая линия».
Некоторые важные или хорошо известные результаты
В pons asinorum или теореме о мосте ослов ‘говорится, что в равнобедренном треугольнике α = β и γ = δ.
Теорема о сумме углов треугольника утверждает, что сумма трех углов любого треугольника, в данном случае углов α, β и γ, всегда будет равна 180усам.
Теорема Пифагора утверждает, что сумма площадей двух квадратов на катетах (a и b) прямоугольного треугольника равна площади квадрата нагипотенузе (c).
Теорема Фалеса утверждает, что если AC — прямой, то угол при B — угол.
Pons Asinorum
В pons asinorum (мост ослов) говорится, что в равнобедренных треугольниках углы при основании равны друг другу, и, если равные прямые линии образуются дальше, тогда углы под основанием равны друг другу. Его название может быть связано с первым его ролью в качестве элемента интеллекта читателя и в последующем более сложным предложением. Он также может быть назван такиз-за сходства геометрической фигуры с крутым мостом, который может пройти только уверенный осел.
Конгруэнтность треугольников

Треугольники конгруэнтны, если у нихвсе три стороны равны (SSS), две стороны и угол между ними равны (SAS), или два угла и сторона (ASA) (Книга I, предложения 4, 8 и 26). Треугольники с тремя равными углами похожи, но не обязательно совпадают. Кроме того, треугольники с двумя равными сторонами и прилегающим углом не обязательно равны или конгруэнтны.
Сумма углового треугольника
Сумма треугольника равна прямому углу (180 градусов). Это приводит к тому, что равносторонний треугольник имеет три внутренних угла в 60градусов. Кроме того, это приводит к тому, что каждый треугольник имеет как минимум два острых угла и до одного тупого или прямого угла.
Теорема Пифагора
Знаменитая теорема Пифагора (книга I, предложение 47) утверждает, что в любом прямом треугольнике площади квадрата, сторона которого является гипотенузой (сторона, противоположная сторона), равна сумме площадей квадратов, стороны которых являются двумя катетами. (две стороны, которые встречаются под прямымуглом).
Теорема Фалеса
Теорема Фалеса, названная в честь Фалеса Милетского, гласит, что если A, B и C являются точками на окружности, где прямая AC диаметр окружности, то угол ABC — прямой угол. Кантор предположил, что Фалес доказал свою теорему с помощью Евклида, книга I, предложение 32, по манере Евклида, книга III, предложение 31.
Масштабирование площади и объема
В современной терминологии, площадь плоской фигуры пропорциональна квадрату любогоиз еелинейных размеров, A ∝ L 2 { displaystyle A propto L ^ {2}}

Приложения
Из-зафундаментального статуса евклидовой геометрии в математике, здесь нецелно давать более репрезентативную выборку приложений.
Геодезист использует уровень
Упаковка сфер применяется к стопке апельсинов.
Параболическое зеркало фокусирует параллельные лучи света.
Как следует из этойологии, одной из причин причинения к геометрии было геодезия и некоторые практические результаты евклидовой геометрии, такие как прямоугольности 3-4-5, использовались задолго дотого, как они были формально доказаны. Основными типами измерений в евклидовой геометрии являются расстояния и углы, оба из которых могут быть измерены непосредственно геодезистом. Исторически сложилось так, что расстояния часто измерялись с помощью цепочек, таких как цепь Гюнтера, а углы — с помощью градуированных окружностей, а теодолита.
Применение евклидовой твердотельной геометрии — определение, такие как проблема упаковки наиболее эффективной сфер в nизмерениях. Эта проблема находит применение в обнаружении и исправлении ошибок..
Геометрическая оптика использует евклидову геометрию для анализа фокусировки света линзами и зеркалами.
Геометрия используется в искусстве и источнике энергии.
Водонапорная башня состоит из конуса, цилиндра и полусферы. Его объем можно рассчитать, используя твердотельную геометрию.
Геометрию можно использовать для дизайна оригами.
Геометрия широко используется в городуре.
Геометрия может быть для проектирования оригами. Некоторые классические задачи построения геометрии невозможно с помощью циркуля и линейки, но их можно решить с помощью оригами.
Довольно много САПР (автоматизированное проектирование) и CAM (автоматизированное производство) основан на евклидовой геометрии. Геометрия дизайна обычно состоит из форм, ограниченных плоскостей, цилиндрами, конусами, торами и т. Д. В настоящее время CAD / CAM играетважную роль при проектировании почти, включая автомобили, самолеты, корабли и смартфоны. Несколько десятилетий назад опытные рисовальщики изучили довольно продвинутую евклидову геометрию, включая такие вещи, как теорема Паскаля и теорема Брианшона. Теперь в этом нет необходимости, потому что все геометрические построения выполняются программы САПР.
В описании структуры пространства
Евклид считал, что его аксиомы были самоо очевидными утверждениями о физической реальности.Доказательства Евклида, основанные на предположениях, возможно, не очевидные в фундаментальных аксиомах Евклида, в частности, о том, что движения фигур не меняют их геометрических свойств, таких как длина и внутренние углы, так называемые евклидовы движения, которые включают в себя размер, отражение и вращения. фигур. Постулат 2 (продолжение линии), взятый как физическое описание пространства, утверждает, что пространство не имеет дыр или границ (другими словами, пространство однородно инеограниченно ); постулат 4 (равенство прямых углов) гласит, что пространство изотропно и место фигуры могут перемещаться в любое, сохраняя конгруэнтность ; и постулат 5 (параллельный постулат ), что пространство плоское (не имеет внутренней кривизны ).
Как более подробно обсуждается ниже, теория Альберта Эйнштейна теории относительности значительно определяет
Неоднозначный характер аксиом, установленные Евклидом, позволяеткомментаторам расходиться во мнениях относительно других последствий для структуры, например, о, или нет, он бесконечен (см. Ниже) и какова его топология. Современные, более строгие переформулировки системы обычно стремятся к более четкому разделу этого более современного подхода, аксиомы 1-4 согласованы либо с бесконечным, либо с конечным пространством. эллиптической геометрии ), и все пять аксиом согласованы с множеством топологий (например, плоскость, цилиндр или тор для двумерной евклидовой геометрии).
Более поздня я работа
Архимед и Аполлониу s

Архимед (ок. 287 г. до н. Э. — ок. 212 г. до н. Э.), Красочная фигура, которая содержит множество исторических анекдотов, вспоминается вместе с Евклидом как один из величайших математиков древности. Хотя основы его работы были заложены Евклидом, его работы, вотличие от Евклида, считаются полностью оригинальными. Он доказал фигур в двух измерениях и провозгласил свойство Архимеда конечных чисел.
Аполлоний Пергский (ок. 262 г. до н. Э. — ок. 190 г. до н. Э.) В основном известен своими исследованиями конических сечений.

17 век: Декарт
Рене Декарт (1596–1650) разработал аналитическую геометрию, альтернативный метод формализации геометрии, которыйсфокусирован на превращении геометрии в алгебру.
В этом подходе точка на плоскости представлена ее декартовыми (x, y) координатами, линия представлена ее уравнением и поэтому на.
В первоначальном подходе Евклида теорема Пифагора следует из аксиом Евклида. В декартовом подходе аксиомы являются аксиомами алгебры, а уравнение, выражающее теорему Пифагора, является определением одного из терминов в аксиомах Евклида, которые теперь считаются теоремами.
Уравнение
- | P Q | знак равно (px — qx) 2 + (py — qy) 2 { displaystyle | PQ | = { sqrt {(p_ {x} -q_ {x}) ^ {2} + (p_ {y} -q_ {y}) ^ {2}}} ,}
определение расстояния между двумя точками P = (p x, p y) и Q = (q x, q y) тогда называется евклидовой метрикой, другие метрики определяют неевклидову геометрию.
С точки зрения ограничения аналитической геометрии Классическая геометрия для циркуля и линейки ограничения уравнениямипервого и второго порядка, например, y = 2x + 1 (линия) или x + y = 7 (круг).
Также в 17 веке Жирар Дезарг, руководствуясь теорией перспективы, представил концепцию идеальных точек, линий и плоскостей, находящихся на бесконечности. Результат можно рассматривать как обобщенную геометрию, проективной геометрии, но его также можно использовать для получения доказательств в обычной евклидовой геометрии, в которой количество частных сокращено.

18 век
Геометры 18 века изо всех сил пытались определить границы Евклидова система. Многие тщетно пытались доказать пятый постулат из первых четырех. К 1763 году было опубликовано по крайней мере 28 различных доказательств, но все они были признаны неверными.
Вплоть до этогопериода геометрии также пытались определить, какие конструкции могут быть выполнены в евклидовой геометрии. Например, проблема деления угла на три части с помощью циркуля и линейки проблема, которая естественным образом возникает в рамках теории, поскольку аксиомы являются к конструктивным операциям, которые могут быть выполнены с помощью этих инструментов. Однако столетия не помогло найти решение этой проблемы, пока Пьерцель не опубликовал в 1837 году доказательствоневозможности такой конструкции. Другие конструкции, которые оказались невозможными, включают удвоение куба и квадрат круга. В случае применения куба невозможность построения из-за того, что методика циркуво и линейки включает уравнения, порядок которых происходит смертью степению, в то время как удвоение куба требует решения двойного порядка.
Эйлер обобщенное обобщение евклидовой геометрии, называемое аффинной геометрией, которое сохраняет пятый постулатнымизменением, в то же время ослабляя постулаты три и четыре таким образом, чтобы исключить понятие угла (из-за чего прямоугольные треугольники теряют смысл) и равенства длины отрезков в целом (из-за чего круги становятся бессмысленными) при сохранении понятий параллелизма как эквивалентности между прямыми и длины длины параллельных отрезков (таким образом, отрезки имеют среднюю точку).
XIX век и неевклидова геометрия

В начале XIX века Карно и Мебиус систематически развивал использование знаковых углов и отрезков прямых как способ упрощения и объединения.
Наиболее значительный прогресс в геометрии века произошел, когда, примерно в 1830 году, Янош Бойяи и Николай Иванович Лобачевский отдельно опубликовал работу по неевклидовой геометрии, в параллельный постулат не действует. Неевклидова геометрия предположа с евклидовой геометрией, постулатпараллельности не может быть доказан с помощью других постулатов.
В 19 веке было также осознано, что десяти аксиом и общих понятий Евклида недостаточно для доказательства всех теорем, изложенных в Элементах. Например, Евклид неявно предполагал, что любая линия содержит по крайней мере две точки, но это предположение не может быть доказано с помощью других аксиом и, следовательно, должно быть само аксиомой. Самое первое геометрическое доказательство в элементе, показанное на рисункевыше, в том. Евклид строит это обычным образом, рисуя круги вокруг конечных точек и скорость их пересечения в качестве вершины третьей . Его аксиомы, однако, не гарантируют, что круги действительно пересекаются, потому что они не утверждают геометрическое свойство непрерывности, которое в декартовых терминах эквивалентно свойству полноты вещественных чисел. Начиная с Морица Паша в 1882 году, было предложено много усовершенствованных аксиоматических систем для геометрии,наиболее известными из которых являются системы Гильберта, Джорджа Биркгофа и Тарский.
20 век и теория относительности

Теория специальной теории относительности Эйнштейна включает четырехмерное пространство-время, пространство Минковского, которое является неевклидовым. Это показывает, что неевклидовы геометрии, которые были введены несколькими годами ранее для демонстрации невозможности доказательства параллельного постулата, также полезны дляописания физического мира.
Однако трехмерная «пространственная часть» пространства Минковского остается пространством евклидовой геометрии. Это не относится к общей теории относительности, для которой геометрия пространственной части пространства-времени не является евклидовой геометрией. Например, если треугольник состоит из трех лучей света, то в целом внутренние углы не составляют в сумме 180 градусов из-за силы тяжести. Относительно слабое гравитационное поле, такое какземное или солнечное, представлено метрикой, которая приблизительно, но не совсем, евклидова. До 20 века не существовало технологии, способной обнаруживать отклонения от евклидовой геометрии, но Эйнштейн предсказал, что такие отклонения будут. Позже они были подтверждены наблюдениями, такими как небольшое искривление звездного света Солнцем во время солнечного затмения в 1919 году, и теперь такие соображения являются неотъемлемой частью программного обеспечения, работающего с системой GPS.
Обработка бесконечности
Бесконечные объекты
Евклид иногда явно различал «конечные линии» (например, постулат 2) и «бесконечные линии» (книга I, утверждение 12). Однако он обычно не делал таких различий, если они не были необходимы. Постулаты явно не относятся к бесконечным линиям, хотя, например, некоторые комментаторы интерпретируют постулат 3, существование круга любого радиуса, как подразумевающий, что пространство бесконечно.
Понятие бесконечно малых величин had previously been discussed extensively by the Eleatic School, but nobody had been able to put them on a firm logical basis, with paradoxes such as Zeno’s paradox occurring that had not been resolved to universal satisfaction. Euclid used the method of exhaustion rather than infinitesimals.
Later ancient commentators, such as Proclus (410–485 CE), treated many questions about infinity as issues demanding proof and, e.g., Proclusутверждал, что доказал бесконечную делимость прямой, основываясь на доказательстве от противоречия, в котором он рассмотрел случаи четного и нечетного числа точек, составляющих ее.
На рубеже 20-го века Отто Штольц, Поль дю Буа-Реймон, Джузеппе Веронезе и другие подготовили противоречивые работы по неархимедовым моделям евклидовой геометрии, в которых расстояние между двумя точками может быть бесконечным или бесконечно малым, в пределах Ньютона — Лейбница смысл. Пятьдесят лет спустя Авраам Робинсон обеспечил строгую логическую основу для работы Веронезе.
Бесконечные процессы
Одна из причин того, что древние считали параллельный постулат менее достоверным, чем другие заключается в том, что физическая проверка потребует от нас осмотра двух линий, чтобы убедиться, что они никогда не пересекались, даже в какой-то очень удаленной точке, и эта проверка потенциально может занять бесконечное количествовремени.>доказательство индукция не развивалась до 17 века, но некоторые более поздние комментаторы считают ее неявной в некоторых доказательствах Евклида, например, доказательстве бесконечности простых чисел.
Предполагаемые парадоксы, включающие бесконечные ряды, такие как Парадокс Зенона, предшествующий Евклиду. Евклид избегал таких обсуждений, дав, например, выражение для частичных сумм геометрического ряда в IX.35, не комментируя возможность позволить количествучлен стать бесконечным.
уриес. Роль примитивных понятий или неопределенных понятий была четко обозначена Алессандро Падоа из делегации Пеано на конференции 1900 года в Париже:
… Когда мы начинаем формулировать теорию, мы можем представить, что неопределенные символы полностью лишены смысла и что недоказанные утверждения — это просто условия, наложенные на неопределенные символы.
Тогда система идей, которую мы выбрали изначально, просто одна интерпретация неопределенных символов; но… эту интерпретацию может игнорировать читатель, который волен заменить ее в своем уме другой интерпретацией… которая удовлетворяет условиям…
Таким образом, логические вопросы становятся полностью независимыми от эмпирических или психологических вопросов….
Затем систему неопределенных символов можно рассматривать как абстракцию, полученную из специализированных теорий, которые возникают, когда… система неопределенных символов последовательно заменяется каждой из интерпретаций…
— Падоа, Essai d’une théorie algébrique des nombre entiers, avec une Introduction logique à une théorie déductive quelconque
То есть математика — это контекстно-независимое знание в иерархической структуре. Как сказал Бертран Рассел :
. Если наша гипотеза о чем-то, а не о каких-то одной или нескольких конкретных вещах, то наши выводы составляют математику. Таким образом, математику можно определить как предмет, в котором мы никогда не знаем, о чем мыговорим, и о том, являетсяли то, что мы говорим, правдой.
— Бертран Рассел, Математика и метафизики
Такие фундаментальные подходы варьируются между фундаментализм и формализм.
Аксиоматическая формулировки
Геометрия — это наука о правильном рассуждении о неправильных числах.
— Джордж Полиа, Как решить, с. 208
- Аксиомы Евклида: В своей диссертации в Тринити-колледже в Кембридже Бертран рассел резюмировал изменяющуюся роль геометрии Евклида в умахфилософов до того времени. Это былконфликт между определенным знанием, независимым от эксперимента, и эмпиризмом, требующим экспериментального ввода. Этот вопрос стал ясен, когда было обнаружено, что параллельный постулат не обязательно действителен, и его применимость была эмпирическим вопросом, решающим, была ли применима геометрия евклидовой или неевклидовой.
- аксиомами Гильберта 6>: Аксиомы Гильберта преследовали цель определить простой и полный набор независимых аксиом, изкоторых можно извлечь наиболееважные геометрические теоремы. Выдающиеся цели заключаются в, чтобы сделать евклидову геометрию (избегая скрытых предположений) и прояснить разветвления параллельного постулата.
- Аксиомы Биркгофа : Биркгоф четыре постулата для евклидовой геометрии, которые могут быть подтверждены экспериментально с помощью шкалы и транспортира.. Эта система во многом полагается на свойства действительных чисел. Понятия угла и расстояния примитивными понятиями.
- Аксиомы Тарского : Альфред Тарский (1902–1983) и его ученики определили элементарную евклидову геометрию как геометрию, которая может быть выражена в логика первого порядка и не зависит от теории множеств в качестве своей основы, в отличие от аксиом Гильберта, которые включают точечные логические основы. Тарский доказал, что его аксиоматическая формулировка элементарной евклидовой геометрии непротиворечива и полна в определенном смысле : алгоритм, которыйдля каждого предложения можетбыть либо истинным, либо ложным. (Это не нарушает теорему Гёделя, потому что евклидова геометрия не может описать достаточное количество арифметики для применения теоремы.) Это эквивалентно разрешимости вещественного замкнутого поля, из элемента которых евклидова геометрия является частью модели.
См. также
- Абсолютная геометрия
- Аналитическая геометрия
- аксиомы Биркгофа
- декартова система координат
- аксиомыГильберта
- падающая геометрия
- Список программ для интерактивной геометрии
- Метрическое пространство
- Неевклидова геометрия
- Упорядоченная геометрия
- Параллельный постулат
- Теория типов
Классические теоремы
- Теорема о биссектрисе угла
- Бабочка теорема
- теорема Чевы
- формула Герона
- теорема Менелая
- девятиточный круг
- теорема Пифагора
Примечания
Литература
- Болл, WW Роуз (1960). Краткое изложение историиматематики (4-е изд. [Перепечатка.Оригинальная публикация: Лондон: Macmillan Co., 1908] изд.). Нью-Йорк: Dover Publications. С. 50–62. ISBN 0-486-20630-0 .
- Коксетер, H.S.M. (1961). Введение в геометрию. Нью-Йорк: Wiley.
- Евс, Ховард (1963). Обзор геометрии (Том первый). Аллин и Бэкон.
- Хит, Томас Л. (1956). Тринадцать книг Евклида (2-е изд. [Факсимиле. Оригинальная публикация: Cambridge University Press, 1925] изд.). Нью-Йорк: Dover Publications.В 3-х томах: т. 1 ISBN 0-486-60088-2 , т. 2 ISBN 0-486-60089-0 , т. 3 ISBN 0-486-60090-4 . Авторитетный перевод Хита Элементов Евклида, а также его обширные исторические исследования и подробные комментарии по всему тексту.
- Миснер, Чарльз У. ; Торн, Кип С. ; Уиллер, Джон Арчибальд (1973). Гравитация. W.H. Фримен.
- Млодинов (2001). Окно Евклида. Свободная пресса.
- Нагель, Э.;Ньюман, Дж. Р. (1958). ДоказательствоГёделя. Издательство Нью-Йоркского университета.
- Тарски, Альфред (1951). Метод принятия решений для элементарной алгебры и геометрии. Univ. Калифорнийской прессы.
Внешние ссылки
| На Викискладе есть материалы, связанные с евклидовой геометрией . |
- , Энциклопедия математики, EMS Press, 2001 [1994]
- , Энциклопедия математики, EMS Press, 2001 [1994]
- Киран Кедлая, Geometry Unbound (обработкас использованием аналитической геометрии;формат PDF, лицензия GFDL)
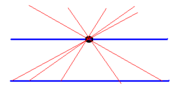
Пересечения прямых (анимация)
Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида [1]:
И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.
Оригинальный текст (др.-греч.)
Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν, ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες.
— ΣTOIXEIA EΥKΛEI∆OΥ
Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. В классическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.
На современном языке текст Евклида можно переформулировать так:
Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей.
Содержание
- 1 Эквивалентные формулировки
- 2 Попытки доказательства
- 3 Первые наброски неевклидовой геометрии
- 4 Открытие неевклидовой геометрии
- 5 Примечания
- 6 Литература
- 7 Ссылки
Эквивалентные формулировки
В школьных учебниках обычно приводится другая формулировка, эквивалентная (равносильная) V постулату и принадлежащая Проклу [2]:
Постулат Прокла
Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых кажутся довольно очевидными. Вот некоторые из них [3]:
- Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые.
- Существуют подобные, но не равные треугольники.
- Любую фигуру можно пропорционально увеличить.
- Существует треугольник сколь угодно большой площади.
- Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны.
- Если две прямые в одну сторону расходятся, то в другую — сближаются.
- Сближающиеся прямые рано или поздно пересекутся.
- Существуют такие прямые, что расстояние от точек одной до другой постоянно.
- Если две прямые начали сближаться, то невозможно, чтобы они затем начали (в ту же сторону, без пересечения) расходиться.
- Сумма углов одинакова у всех треугольников.
- Существует треугольник, сумма углов которого равна двум прямым.
- Существуют параллельные прямые, причём две прямые, параллельные третьей, параллельны и друг другу.
- Существуют параллельные прямые, причём прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую.
- Для всякого невырожденного треугольника существует описанная окружность.
- Вариант: через любые три точки можно провести либо прямую, либо окружность.
- Справедлива теорема Пифагора.
Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему.
Если из списка аксиом исключить V постулат, то полученная система аксиом будет описывать так называемую абсолютную геометрию.
Если вместо V постулата допустить, что для пары точка—прямая V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все вышеперечисленные эквивалентные утверждения неверны.
Система аксиом сферической геометрии требует изменения также и других аксиом Евклида.
Попытки доказательства
Пятый постулат резко выделяется среди других, вполне очевидных (см. Начала Евклида). Он больше похож на сложную, неочевидную теорему. Евклид, вероятно, сознавал это, и поэтому первые 28 предложений в «Началах» доказываются без его помощи.
Математики с давних времён пытались «улучшить Евклида» — либо исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы, либо заменить его другим, столь же очевидным, как другие постулаты. Надежду на достижимость этого результата поддерживало то, что IV постулат Евклида (все прямые углы равны) действительно оказался лишним — он был строго доказан как теорема и исключён из перечня аксиом.
За два тысячелетия было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг: оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же пятого постулата.
Прокл (V век н. э.) в «Комментарии к I книге Начал Евклида» сообщает, что такое доказательство предложил Клавдий Птолемей, критикует его доказательство и предлагает своё собственное, опираясь на допущение, что расстояние между двумя непересекающимися прямыми есть ограниченная величина. Впоследствии выяснилось, что это допущение равносильно V постулату.
После упадка античной культуры V постулатом занялись математики стран ислама. Доказательство ал-Джаухари, ученика ал-Хорезми (IX век) [4], неявно подразумевало: если при пересечении двух прямых какой-либо третьей накрест-лежащие углы равны, то то же имеет место при пересечении тех же двух прямых любой другой. И это допущение равносильно V постулату.
Сабит ибн Курра (IX век) дал два доказательства; в первом он опирается на предположение, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. Во втором — исходит из существования равноотстоящих прямых, причём этот факт ибн Курра пытается вывести из представления о «простом движении», т. е. о равномерном движении на фиксированном расстоянии от прямой (ему представляется очевидным, что траектория такого движения — тоже прямая) [5]. Каждое из двух упомянутых утверждений Ибн Курры эквивалентно V постулату.
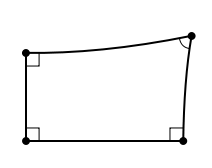
Четырёхугольник Ламберта
Аналогичную ошибку сделал ибн ал-Хайсам, но он впервые рассмотрел фигуру, позже получившую название «четырёхугольник Ламберта» — четырёхугольник, у которого три внутренних угла — прямые. Он сформулировал три возможных варианта для четвёртого угла: острый, прямой, тупой. Обсуждение этих трёх гипотез, в разных вариантах, многократно возникало в позднейших исследованиях.
Поэт и математик Омар Хайям подверг критике попытки ввести в геометрию механическое движение. Он предложил заменить V постулат на другой, более простой: две сходящиеся прямые пересекаются, и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Каждая из двух частей этого утверждения равносильна постулату Евклида [6].
Ал-Абхари предложил доказательство, сходное с доказательством ал-Джаухари. (Это доказательство приводит в своей книге ас-Самарканди, и ряд исследователей считал его доказательством ас-Самарканди.) Он исходит из верного в абсолютной геометрии утверждения о том, что для всякой прямой, пересекающей стороны данного угла, может быть построена ещё одна прямая, пересекающая стороны этого же угла и отстоящая от его вершины дальше, чем первая. Но из этого утверждения он делает логически необоснованный вывод о том, что через всякую точку внутри данного угла можно провести прямую, пересекающую обе стороны этого угла, — и основывает на этом последнем утверждении, эквивалентном V постулату, всё дальнейшее доказательство.
Насир ад-Дин ат-Туси предложил построение, аналогичное построению Омара Хайяма [7]. Отметим, что сочинения ат-Туси стали известны Джону Валлису, и тем самым сыграли роль в развёртывании исследований по неевклидовой геометрии в Европе.
Первую в Европе известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Герсонид (он же Леви бен Гершом, XIV век). Его доказательство опиралось на утверждение о существовании прямоугольника [8].
К XVI веку относится доказательство учёного-иезуита Христофора Клавиуса. Доказательство его, как и у ибн Курры, основывалось на утверждении, что линия, равноотстоящая от прямой — тоже прямая [9].
Валлис в 1693 году в одной из своих работ воспроизводит перевод сочинения ат-Туси и предлагает эквивалентную, но более простую формулировку: существуют подобные, но не равные фигуры [10]. Клеро в своих «Началах геометрии» (1741), как и Герсонид, вместо V постулата взял его эквивалент «существует прямоугольник».
В целом можно сказать, что все перечисленные попытки принесли немалую пользу: была установлена связь между V постулатом и другими утверждениями, были отчётливо сформулированы две альтернативы V постулату — гипотезы острого и тупого угла.
Первые наброски неевклидовой геометрии
Сочинение Саккери
Глубокое исследование V постулата, основанное на совершенно оригинальном принципе, провёл в 1733 году итальянский монах-иезуит, преподаватель математики Джироламо Саккери. Он опубликовал труд под названием «Евклид, очищенный от всех пятен, или же геометрическая попытка установить самые первые начала всей геометрии». Идея Саккери состояла в том, чтобы заменить V постулат противоположным утверждением, вывести из новой системы аксиом как можно больше следствий, тем самым построив «ложную геометрию», и найти в этой геометрии противоречия или заведомо неприемлемые положения. Тогда справедливость V постулата будет доказана от противного [11].
Саккери рассматривает всё те же три гипотезы о 4-м угле четырёхугольника Ламберта. Гипотезу тупого угла он отверг сразу по формальным соображениям. Легко показать, что в этом случае вообще все прямые пересекаются, а тогда можно заключить, что V постулат Евклида справедлив — ведь он как раз и утверждает, что при некоторых условиях прямые пересекаются. Отсюда делается вывод, что «гипотеза тупого угла всегда целиком ложна, так как она сама себя разрушает» [12].
После этого Саккери переходит к опровержению «гипотезы острого угла», и здесь его исследование гораздо интереснее. Он допускает, что она верна, и, одно за другим, доказывает целый ряд следствий. Сам того не подозревая, он продвигается довольно далеко в построении геометрии Лобачевского. Многие теоремы, доказанные Саккери, выглядят интуитивно неприемлемыми, но он продолжает цепочку теорем. Наконец, Саккери доказывает, что в «ложной геометрии» любые две прямые или пересекаются, или имеют общий перпендикуляр, по обе стороны от которого они удаляются друг от друга, или же удаляются друг от друга с одной стороны и неограниченно сближаются с другой. В этом месте Саккери делает неожиданный вывод: «гипотеза острого угла совершенно ложна, так как противоречит природе прямой линии» [13].
Видимо, Саккери чувствовал необоснованность этого «доказательства», потому что исследование продолжается. Он рассматривает эквидистанту — геометрическое место точек плоскости, равноотстоящих от прямой; в отличие от своих предшественников, Саккери знает, что в рассматриваемом случае это вовсе не прямая. Однако, вычисляя длину её дуги, Саккери допускает ошибку и приходит к реальному противоречию, после чего заканчивает исследование и с облегчением заявляет, что он «вырвал эту зловредную гипотезу с корнем».
Во второй половине XVIII века было опубликовано более 50 работ по теории параллельных. В обзоре тех лет (Г. С. Клюгель) исследуется более 30 попыток доказать V постулат и доказывается их ошибочность. Известный немецкий математик и физик И. Г. Ламберт, с которым Клюгель переписывался, тоже заинтересовался проблемой; его «Теория параллельных линий» была издана посмертно в 1786 году.
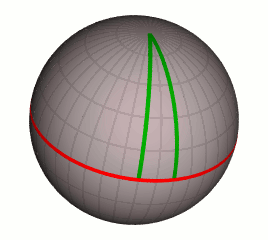
Сферическая геометрия: все прямые пересекаются
Ламберт первым обнаружил, что «геометрия тупого угла» реализуется на сфере, если под прямыми понимать большие круги. Он, как и Саккери, вывел из «гипотезы острого угла» множество следствий, причём продвинулся гораздо дальше Саккери; в частности, он обнаружил, что дополнение суммы углов треугольника до 180° пропорционально площади треугольника.
В своей книге Ламберт проницательно отметил [14]:
Мне кажется очень замечательным, что вторая гипотеза [тупого угла] оправдывается, если вместо плоских треугольников взять сферические. Я из этого почти должен был бы сделать вывод — заключение, что третья гипотеза имеет место на какой-то мнимой сфере. Во всяком случае, должна же существовать причина, почему она на плоскости далеко не так легко поддаётся опровержению, как это могло быть сделано в отношении второй гипотезы.
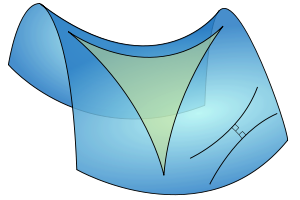
Геометрия на поверхности отрицательной кривизны
Ламберт не нашёл противоречия в гипотезе острого угла и пришёл к заключению, что все попытки доказать V постулат безнадёжны. Однако в ложности «геометрии острого угла» он не сомневался.
Тем временем попытки «смыть пятна» с Евклида продолжались (Луи Бертран, Лежандр и другие). Лежандр дал целых три доказательства V постулата, ошибочность которых быстро показали его современники [15]. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии.
Открытие неевклидовой геометрии
В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К. Ф. Гаусс, Н. И. Лобачевский и Я. Бойяи. Но цель у них была уже иная — не разоблачить неевклидову геометрию как невозможную, а, наоборот, построить альтернативную геометрию и выяснить её возможную роль в реальном мире. На тот момент это была совершенно еретическая идея; никто из учёных ранее не сомневался, что физическое пространство евклидово. Интересно, что Гаусса и Лобачевского учил в молодости один и тот же учитель — Мартин Бартельс.
Первым был Гаусс. Он не публиковал никаких работ на эту тему, но его черновые заметки и несколько писем однозначно подтверждают его понимание неевклидовой геометрии. В 1818 году в письме к австрийскому астроному Герлингу он писал [16]:
Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову.
Ознакомившись с работой Лобачевского «Геометрические исследования по теории параллельных», Гаусс энергично ходатайствует об избрании русского математика иностранным членом-корреспондентом Гёттингенского королевского общества (что и произошло в 1842 году).
Евклид
Н. И. Лобачевский
Лобачевский и Бойяи проявили бо́льшую смелость, чем Гаусс, и почти одновременно (около 1830 года), независимо друг от друга, опубликовали изложение того, что сейчас называется геометрией Лобачевского. Лобачевский продвинулся в исследовании новой геометрии дальше всех, и она в настоящий момент носит его имя. Но главная его заслуга не в этом, а в том, что он поверил в новую геометрию и имел мужество отстаивать своё убеждение (он даже предложил экспериментально проверить V постулат, измерив сумму углов треугольника) [17].
Трагическая судьба Лобачевского, подвергнутого остракизму в научном мире и служебном окружении за слишком смелые мысли, показала, что опасения Гаусса были не напрасны. Но и его борьба была не напрасна. Спустя несколько десятилетий математики (Бернхард Риман), а затем и физики (Общая теория относительности, Эйнштейн), окончательно покончили с догматом об евклидовой геометрии физического пространства.
Доказать непротиворечивость новой геометрии ни Лобачевский, ни Бойяи не сумели — тогда математика ещё не располагала необходимыми для этого средствами. Только спустя 40 лет появились модель Клейна и другие модели, реализующие аксиоматику геометрии Лобачевского на базе евклидовой геометрии. Эти модели убедительно доказывают, что отрицание V постулата не противоречит остальным аксиомам геометрии; отсюда вытекает, что V постулат независим от остальных аксиом и доказать его невозможно.
Примечания
- ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
- ↑ Euclid’s Fifth Postulate
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
- ↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и примечания Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
- ↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М.: 1962.
- ↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, примечания Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
- ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
- ↑ Clavius C. Euclidis Elementorum, libri XV. — Romae: 1574.
- ↑ Wallis. Opera mathematica, v. II. — Oxoniae: 1693. — С. 665.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig: 1895. — С. 100.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig: 1895. — С. 105.
- ↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin: 1781—1784. — С. 202—203.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 218.
- ↑ Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М.: ГИТТЛ, 1956. — С. 119-120.
- ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949.
Литература
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. ГИФМЛ, 1960. 468 с.
- Гильберт Д. Основания геометрии. — Л., «Сеятель», 1923. 152 с.
- «Начала» Евклида
- История математики с древнейших времён до начала XIX столетия (под ред. А. П. Юшкевича), тома I—III, М., Наука, 1972.
- Каган В. Ф. Геометрия Лобачевского и её предыстория. М.—Л., 1949. (Основания геометрии, ч. 1).
- Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. М.: Наука, 1976.
- Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. М.: Наука, 1983.
- Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. М., 1968 (серия «Эврика»).
- Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. М., 1956.
Ссылки
- Пятый постулат Евклида
Wikimedia Foundation.
2010.
Пересечения прямых
Аксиома параллельности Евклида или пятый постулат — одна из аксиом, лежащих в основании классической планиметрии впервые описанной в «Началах Евклида».
Шаблон:Начало цитаты
И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.
Шаблон:Конец цитаты
Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах Начал Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает их порядок. В современном издании Гейберга сформулированное утверждение является пятым постулатом.
На современном языке:
Шаблон:Начало цитаты
Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей.
Шаблон:Конец цитаты
Эквивалент аксиомы:
Шаблон:Начало цитаты
В плоскости через точку, не лежащую на данной прямой, можно провести одну, и только одну прямую, параллельную данной.
Шаблон:Конец цитаты
В геометрии Лобачевского вместо нее используется аксиома: «в плоскости через точку, не лежащую на данной прямой, можно провести по крайней мере две прямые, не пересекающиеся с данной», что позволяет создать альтернативную внутренне логически непротиворечивую систему.
Попытки доказательства
Пятый постулат выглядел более сложным, чем остальные исходные утверждения, кроме того, первые 26 предложений в «Началах» доказываются без его помощи. Математики с древних времён пытались исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы.
За много веков было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг (лат. circulus in demonstrando): оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же 5-го постулата.
Прокл (V век н. э.), опирался в своем доказательстве на допущение, что расстояние между двумя непересекающимися прямыми есть ограниченная величина; впоследствии выяснилось, что это допущение равносильно пятому постулату.
Первую известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Лев Гарсонид (или Леви бен Гершон) (1288—1344). Его доказательство опиралось на утверждение о существовании прямоугольника.
К XVI веку относится доказательство учёного-иезуита Христофора Клавия. Доказательство основывалось на утверждении, что линия, равноотстоящая от прямой — тоже прямая.
После открытия Н. И. Лобачевским и Я. Бояи неевклидовой геометрии и доказательства её непротиворечивости стало ясно, что доказать пятую аксиому Евклида невозможно.
Литература
- Начала Евклида. Книги I-VI. М.-Л., 1950
- Гильберт Д. Основания геометрии. — Л., «Сеятель», 1923. 152 с.
da:Euklids postulater
fa:اصل پنجم اقلیدس
he:אקסיומת המקבילים
nl:Parallellenpostulaat
pl:Postulat równoległości
sr:Пети постулат
sv:Parallellaxiomet
vi:Tiên đề Euclid về đường thẳng song song
Если сумма внутренних углов α и β меньше 180 °, две прямые линии, образованные бесконечно, пересекаются на этой стороне.
В геометрия, то параллельный постулат, также называемый Евклид пятый постулат потому что это пятый постулат в Евклида Элементы, является отличительной аксиома в Евклидова геометрия. В нем говорится, что в двумерной геометрии:
Если отрезок пересекает две прямые линии образуя два внутренних угла на одной стороне, которые в сумме составляют менее двух прямые углы, то две прямые, если их удлинить бесконечно, встречаются на той стороне, на которой сумма углов меньше двух прямых углов.
Этот постулат конкретно не говорит о параллельных линиях;[1] это всего лишь постулат, связанный с параллелизмом. Евклид дал определение параллельных прямых в книге I, определение 23.[2] прямо перед пятью постулатами.[3]
Евклидова геометрия изучение геометрии, удовлетворяющее всем аксиомам Евклида, включая постулат параллельности.
Постулат долгое время считался очевидным или неизбежным, но доказательства были неуловимы. В конце концов было обнаружено, что инвертирование постулата дает действительную, хотя и другую геометрию. Геометрия, в которой постулат параллельности не выполняется, известна как неевклидова геометрия. Геометрия независимый пятого постулата Евклида (т. е. предполагает только современный эквивалент первых четырех постулатов) известен как абсолютная геометрия (или иногда «нейтральная геометрия»).
Эквивалентные свойства
Вероятно, самый известный эквивалент параллельного постулата Евклида, зависящий от других его постулатов, — это Аксиома Playfair, названный в честь шотландского математик Джон Плейфэр, в котором говорится:
На плоскости, для которой задана линия и точка не на ней, через точку можно провести не более одной линии, параллельной данной линии.[4]
Сама по себе эта аксиома не логически эквивалентный постулату евклидовой параллели, поскольку существуют геометрии, в которых одно истинно, а другое — нет. Однако при наличии остальных аксиом, которые дают евклидову геометрию, каждая из них может использоваться для доказательства другой, поэтому они эквивалентны в контексте абсолютная геометрия.[5]
Было предложено много других утверждений, эквивалентных постулату параллельности, некоторые из них поначалу кажутся не связанными с параллелизмом, а некоторые кажутся таковыми. самоочевидный что они были бессознательно предполагалось людьми, которые утверждали, что доказали параллельный постулат из других постулатов Евклида. Эти эквивалентные утверждения включают:
- Существует не более одной линии, которую можно провести параллельно другой, проведенной через внешнюю точку. (Аксиома Playfair )
- Сумма углы в каждом треугольник составляет 180 ° (постулат треугольника ).
- Существует треугольник, сумма углов которого составляет 180 °.
- Сумма углов одинакова для всех треугольников.
- Существует пара похожий, но нет конгруэнтный, треугольники.
- Каждый треугольник может быть ограниченный.
- Если три угла четырехугольник находятся прямые углы, то четвертый угол тоже прямой.
- Существует четырехугольник, в котором все углы прямые, т.е. прямоугольник.
- Существует пара прямых, находящихся на постоянном расстоянии расстояние друг от друга.
- Две линии, параллельные одной линии, также параллельны друг другу.
- В прямоугольный треугольник, квадрат гипотенузы равен сумме квадратов двух других сторон (Теорема Пифагора ).[6][7]
- В Закон косинусов, общий случай теоремы Пифагора.
- Верхнего предела для площадь треугольника. (Аксиома Уоллиса )[8]
- Вершинные углы Четырехугольник Саккери равны 90 °.
- Если линия пересекает одну из двух параллельных линий, обе из которых копланарны исходной линии, то она также пересекает другую. (Прокл аксиома)[9]
Однако альтернативы, в которых используется слово «параллельный», перестают казаться такими простыми, когда приходится объяснять, какое из четырех общих определений «параллель» имеется в виду — постоянное разделение, никогда не встречающиеся, те же углы, где пересекаются немного третья линия или те же углы, где пересекается любой третья строка — поскольку эквивалентность этих четырех сама по себе является одним из бессознательно очевидных предположений, эквивалентных пятому постулату Евклида. В приведенном выше списке всегда подразумеваются непересекающиеся линии. Например, если слово «параллель» в аксиоме Плейфэра означает «постоянное разделение» или «одинаковые углы, пересекаемые любой третьей линией», то это больше не эквивалентно пятому постулату Евклида и доказуемо на основе первых четырех. (аксиома гласит: «Существует не более одной линии …», что согласуется с отсутствием таких линий). Однако, если определение взято так, что параллельные прямые — это прямые, которые не пересекаются или у которых есть какая-то линия, пересекающая их под одними и теми же углами, аксиома Плейфэра контекстуально эквивалентна пятому постулату Евклида и, таким образом, логически независима от первых четырех постулатов. Обратите внимание, что последние два определения не эквивалентны, потому что в гиперболической геометрии второе определение справедливо только для ультрапараллельный линий.
История
В течение двух тысяч лет было предпринято множество попыток доказать параллельный постулат, используя первые четыре постулата Евклида. Основная причина того, что такое доказательство так востребовано, заключалась в том, что, в отличие от первых четырех постулатов, параллельный постулат не является самоочевидным. Если порядок, в котором постулаты были перечислены в элементах, важен, это указывает на то, что Евклид включил этот постулат только тогда, когда он понял, что не может доказать его или действовать без него.[10]Было предпринято множество попыток доказать пятый постулат из четырех других, многие из них долгое время принимались в качестве доказательств, пока не была обнаружена ошибка. Неизменно ошибкой было допущение некоторого «очевидного» свойства, которое оказывалось эквивалентным пятому постулату (Аксиома Playfair ). Хотя это известно со времен Прокла, оно стало известно как Аксиома Плейфэра после того, как Джон Плейфэр написал знаменитый комментарий к Евклиду в 1795 году, в котором он предложил заменить пятый постулат Евклида его собственной аксиомой.
Прокл (410–485) написал комментарий к Элементы где он комментирует попытки доказательства вывести пятый постулат из четырех других; в частности, он отмечает, что Птолемей представил ложное «доказательство». Затем Прокл приводит собственное ложное доказательство. Однако он дал постулат, эквивалентный пятому постулату.
Ибн аль-Хайсам (Альхазен) (965-1039), Арабский математик, сделал попытку доказать постулат параллельности с помощью доказательство от противного,[11] в ходе которой он ввел понятие движение и трансформация в геометрию.[12] Он сформулировал Четырехугольник Ламберта, который Борис Абрамович Розенфельд называет «четырехугольником Ибн аль-Хайтама – Ламберта»,[13] и его попытка доказательства содержит элементы, подобные тем, которые были найдены в Четырехугольники Ламберта и Аксиома Playfair.[14]
Персидский математик, астроном, философ и поэт. Омар Хайям (1050–1123), попытался доказать пятый постулат с помощью другого явно заданного постулата (основанного на четвертом из пяти принципы из-за философа (Аристотель ), а именно: «Две сходящиеся прямые линии пересекаются, и две сходящиеся прямые линии не могут расходиться в том направлении, в котором они сходятся».[15] Он получил некоторые из более ранних результатов, принадлежащих эллиптическая геометрия и гиперболическая геометрия, хотя его постулат исключал последнюю возможность.[16] В Четырехугольник Саккери также впервые был рассмотрен Омаром Хайямом в конце 11 века в Книге I Объяснение трудностей постулатов Евклида.[13] В отличие от многих комментаторов Евклида до и после него (включая Джованни Джироламо Саккери ) Хайям пытался доказать не параллельный постулат как таковой, а вывести его из своего эквивалентного постулата. Он признал, что из исключения пятого постулата Евклида возникают три возможности; если два перпендикуляра к одной линии пересекают другую линию, разумный выбор последнего может сделать внутренние углы в месте пересечения двух перпендикуляров равными (тогда он параллелен первой линии). Если эти равные внутренние углы являются прямыми углами, мы получаем пятый постулат Евклида, в противном случае они должны быть либо острыми, либо тупыми. Он показал, что острые и тупые случаи приводят к противоречиям, используя его постулат, но теперь известно, что его постулат эквивалентен пятому постулату.
Насир ад-Дин ат-Туси (1201–1274), в его Аль-рисала аль-шафия’ан аль-шакк фил-хутут аль-мутавазия (Обсуждение, снимающее сомнения относительно параллельных линий) (1250 г.), написал подробную критику параллельного постулата и попытки доказательства Хайяма столетием ранее. Насир ад-Дин попытался получить доказательство, противоречащее параллельному постулату.[17] Он также рассмотрел случаи того, что сейчас известно как эллиптическая и гиперболическая геометрия, хотя и исключил их оба.[16]
Евклидова, эллиптическая и гиперболическая геометрия. Постулат параллельности выполняется только для моделей евклидовой геометрии.
Сын Насира ад-Дина, Садр ад-Дин (иногда известный как «Псевдо-Туси «), написал книгу по этому вопросу в 1298 году, основанную на более поздних мыслях своего отца, в которых был представлен один из самых ранних аргументов в пользу неевклидовой гипотезы, эквивалентной параллельному постулату.» Он существенно пересмотрел как евклидову систему аксиом, так и постулаты. и доказательства многих предложений из Элементы.»[17][18] Его работа была опубликована в Рим в 1594 г. и изучалась европейскими геометрами. Эта работа стала отправной точкой для работы Саккери по этому вопросу.[17] который открылся критикой работ Садр ад-Дина и Уоллиса.[19]
Джордано Витале (1633-1711), в своей книге Евклид реституо (1680, 1686) использовали четырехугольник Хайяма-Саккери, чтобы доказать, что если три точки равноудалены на основании AB и вершине CD, то AB и CD везде равноудалены. Джироламо Саккери (1667-1733) проводил ту же линию рассуждений более тщательно, правильно извлекая абсурдность из тупого случая (исходя, как Евклид, из неявного предположения, что линии могут быть неограниченно продолжены и иметь бесконечную длину), но не опровергая острый случай. (хотя ему удалось ошибочно убедить себя, что это так).
В 1766 г. Иоганн Ламберт написал, но не опубликовал, Theorie der Parallellinien в котором он попытался, как и Саккери, доказать пятый постулат. Он работал с фигурой, которую сегодня мы называем Четырехугольник Ламберта, четырехугольник с тремя прямыми углами (можно рассматривать как половину четырехугольника Саккери). Он быстро исключил возможность того, что четвертый угол тупой, как и Саккери и Хайям, а затем приступил к доказательству многих теорем в предположении об остром угле. В отличие от Саккери, он никогда не чувствовал, что пришел к противоречию с этим предположением. Он доказал неевклидов результат, согласно которому сумма углов в треугольнике увеличивается с уменьшением площади треугольника, и это привело его к размышлениям о возможности модели острого случая на сфере мнимого радиуса. Он не стал продвигать эту идею дальше.[20]
Там, где Хайям и Саккери пытались доказать пятую точку Евклида, опровергнув единственно возможные альтернативы, в девятнадцатом веке математики наконец изучали эти альтернативы и открывали логически последовательный геометрии, которые в результате. В 1829 г. Николай Иванович Лобачевский опубликовал отчет об острой геометрии в малоизвестном русском журнале (позже переиздан в 1840 году на немецком языке). В 1831 г. Янош Бойяи включил в книгу своего отца приложение с описанием острой геометрии, которую, несомненно, он разработал независимо от Лобачевского. Карл Фридрих Гаусс тоже изучал проблему, но не опубликовал ни одного из своих результатов. Услышав о результатах Бойяи в письме от отца Бойяи, Фаркас Бойяи, Гаусс заявил:
«Если бы я начал с того, что сказал, что не могу похвалить эту работу, вы наверняка на мгновение удивитесь. Но я не могу сказать иначе. Хвалить это значило бы хвалить себя. Действительно, все содержание работы, пройденный путь По мнению вашего сына, результаты, к которым его привели, почти полностью совпадают с моими медитациями, которые частично занимали мой ум последние тридцать или тридцать пять лет «.[21]
Полученная геометрия была позже разработана Лобачевский, Риман и Пуанкаре в гиперболическая геометрия (острый случай) и эллиптическая геометрия (тупой случай). В независимость постулата параллельности из других аксиом Евклида был наконец продемонстрирован Эухенио Бельтрами в 1868 г.
Обращение к постулату параллельности Евклида
Обратное к постулату параллельности: если сумма двух внутренних углов равна 180 °, то прямые параллельны и никогда не пересекутся.
Евклид не постулировал разговаривать его пятого постулата, который является одним из способов отличить евклидову геометрию от эллиптическая геометрия. Элементы содержат доказательство эквивалентного утверждения (Книга I, предложение 27): Если прямая линия, падающая на две прямые, уравнивает чередующиеся углы друг с другом, прямые линии будут параллельны друг другу. В качестве Де Морган[22] Как уже отмечалось, это логически эквивалентно (Книга I, предложение 16). Эти результаты не зависят от пятого постулата, но требуют второго постулата.[23] что нарушается в эллиптической геометрии.
Критика
Попытки логически доказать параллельный постулат, а не восьмую аксиому,[24] подверглись критике со стороны Артур Шопенгауэр. Однако аргумент, использованный Шопенгауэром, заключался в том, что постулат очевиден для восприятия, а не в том, что он не был логическим следствием других аксиом.
Смотрите также
- Неевклидова геометрия
Примечания
- ^ неевклидовы геометрии, к Д-р Катрина Пятек-Хименес
- ^ Элементы Евклида, Книга I, Определение 23
- ^ Элементы Евклида, Книга I
- ^ Параллельный постулат Евклида и аксиома Playfair
- ^ Хендерсон и Тайминя 2005, стр. 139
- ^ Эрик В. Вайсштейн (2003), CRC краткая энциклопедия математики (2-е изд.), С. 2147, г. ISBN 1-58488-347-2,
Постулат параллельности эквивалентен Постулат равноудаленности, Аксиома Playfair, Аксиома прокла, то Постулат треугольника и теорема Пифагора.
- ^ Александр Р. Прусс (2006), Принцип достаточной причины: переоценка, Cambridge University Press, стр. 11, ISBN 0-521-85959-X,
Мы могли бы включить … параллельный постулат и вывести теорему Пифагора. Или мы могли бы вместо этого сделать теорему Пифагора среди других аксиом и вывести постулат параллельности.
- ^ Богомольный Александр. «Пятый постулат Евклида». Разрезать узел. Получено 30 сентября 2011.
- ^ Вайсштейн, Эрик В. «Аксиома Прокла — MathWorld». Получено 2009-09-05.
- ^ Флоренс П. Льюис (январь 1920 г.), «История параллельного постулата», Американский математический ежемесячник, The American Mathematical Monthly, Vol. 27, №1, 27 (1): 16–23, Дои:10.2307/2973238, JSTOR 2973238.
- ^ Кац 1998, стр. 269
- ^ Кац 1998, п. 269:
Фактически, этот метод характеризовал параллельные линии как линии, всегда равноудаленные друг от друга, а также ввел понятие движения в геометрию.
- ^ а б Розенфельд 1988, п. 65
- ^ Смит 1992
- ^ Борис Розенфельд и Адольф Ющкевич (1996), Геометрия, стр.467 в Рошди Рашед, Режис Морелон (1996), Энциклопедия истории арабской науки, Рутледж, ISBN 0-415-12411-5.
- ^ а б Борис А. Розенфельд и Адольф П. Юшкевич (1996), «Геометрия», в Рошди Рашед, ред. Энциклопедия истории арабской науки, Vol. 2, стр. 447-494 [469], Рутледж, Лондон и Нью-Йорк:
«Постулат Хайяма исключил случай гиперболической геометрии, тогда как постулат ат-Туси исключил как гиперболическую, так и эллиптическую геометрии».
- ^ а б c Кац 1998, стр.271:
«Но в рукописи, вероятно написанной его сыном Садр ад-Дином в 1298 году на основе более поздних мыслей Насир ад-Дина по этому вопросу, есть новый аргумент, основанный на другой гипотезе, также эквивалентной гипотезе Евклида, […] Важность этой последней работы состоит в том, что она была опубликована в Риме в 1594 году и изучалась европейскими геометрами. В частности, она стала отправной точкой для работ Саккери и, в конечном итоге, для открытия неевклидовой геометрии ».
- ^ Борис А. Розенфельд и Адольф П. Юшкевич (1996), «Геометрия», в Рошди Рашед, ред. Энциклопедия истории арабской науки, Vol. 2, стр. 447-494 [469], Рутледж, Лондон и Нью-Йорк:
«В Экспозиция Евклида псевдо-Туси, […] вместо постулата используется другое утверждение. Он не зависел от постулата Евклида V и его легко доказать. […] Он существенно переработал как евклидову систему аксиом и постулатов, так и доказательства многих утверждений из Элементы.»
- ^ Джованни Джироламо Саккери из MacTutor
- ^ О’Коннор, Дж. Дж .; Робертсон, Э.Ф. «Иоганн Генрих Ламберт». Получено 16 сентября 2011.
- ^ Faber 1983, стр. 161
- ^ Хит, Т.Л., Тринадцать книг Элементов Евклида, Том 1, Дувр, 1956, стр.309.
- ^ Кокстер, H.S.M., Неевклидова геометрия, 6-е изд., MAA 1998, стр.3
- ^ Шопенгауэр имеет в виду общее понятие 4 Евклида: совпадающие друг с другом фигуры равны друг другу.
Рекомендации
- Кэрролл, Льюис, Евклид и его современные соперники, Дувр, ISBN 0-486-22968-8
- Фабер, Ричард Л. (1983), Основы евклидовой и неевклидовой геометрии, Нью-Йорк: Marcel Dekker Inc., ISBN 0-8247-1748-1
- Хендерсон, Дэвид В .; Тайминя, Дайна (2005), Изучение геометрии: евклидова и неевклидова с историей (3-е изд.), Верхняя Сэдл-Ривер, Нью-Джерси: Пирсон Прентис Холл, ISBN 0-13-143748-8
- Кац, Виктор Дж. (1998), История математики: введение, Эддисон-Уэсли, ISBN 0-321-01618-1, OCLC 38199387
- Розенфельд, Борис А. (1988), История неевклидовой геометрии: эволюция концепции геометрического пространства, Springer Science + Business Media, ISBN 0-387-96458-4, OCLC 15550634
- Смит, Джон Д. (1992), «Замечательный Ибн аль-Хайсам», Математический вестник, Математическая ассоциация, 76 (475): 189–198, Дои:10.2307/3620392, JSTOR 3620392
внешняя ссылка
- На горах Гаусса
Эдер, Мишель (2000), Взгляды на параллельный постулат Евклида в Древней Греции и в средневековом исламе, Университет Рутгерса, получено 2008-01-23
Пересечения прямых (анимация)
Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида[1]:
И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.
Оригинальный текст (др.-греч.)
Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν, ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες.
— ΣTOIXEIA EΥKΛEI∆OΥ
Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. В классическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.
На современном языке текст Евклида можно переформулировать так[2]:
Если [на плоскости] при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180°, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше 180°.
Уточнение, с какой именно стороны пересекаются прямые, Евклид добавил, вероятно, для ясности — легко доказать, что оно вытекает из самого факта существования пересечения[2].
Пятый постулат чрезвычайно сильно отличается от других постулатов Евклида, более простых и очевидных (см. Начала Евклида). Поэтому в течение двух тысячелетий не прекращались попытки исключить его из списка аксиом и вывести как теорему. Все эти попытки окончились неудачей. «Вероятно, невозможно в науке найти более захватывающую и драматичную историю, чем история пятого постулата Евклида»[3]. Несмотря на отрицательный результат, эти поиски не были напрасны, так как в конечном счёте привели к полному пересмотру научных представлений о геометрии Вселенной.
Содержание
- 1 Эквивалентные формулировки постулата о параллельных
- 2 Абсолютная геометрия
- 3 Попытки доказательства
- 4 Первые наброски неевклидовой геометрии
- 5 Открытие неевклидовой геометрии
- 6 О доказательстве независимости
- 7 Примечания
- 8 Литература
- 9 Ссылки
Эквивалентные формулировки постулата о параллельных[править | править вики-текст]
В современных источниках обычно приводится другая формулировка постулата о параллельных, эквивалентная (равносильная) V постулату и принадлежащая Проклу[4] (за рубежом её часто называют аксиомой Плейфера):
В этой формулировке слова «одну и только одну» часто заменяют на «только одну» или «не более одной», так как существование хотя бы одной такой параллельной сразу следует из теорем 27 и 28 «Начал» Евклида.
Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых сами по себе кажутся довольно очевидными. Вот некоторые из них[5][6][7].
- Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые[8].
- Существуют подобные, но не равные треугольники (аксиома Валлиса, 1693). И здесь достаточно, чтобы существовала хотя бы одна пара таких треугольников[8].
- Любую фигуру можно пропорционально увеличить.
- Вариант: существует по меньшей мере одна фигура, которую можно пропорционально увеличить.
- Существует треугольник сколь угодно большой площади.
- Прямая, проходящая через точку внутри угла, пересекает по крайней мере одну его сторону (аксиома Иоганна Фридриха Лоренца, 1791).
- Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны (одно из предположений Лежандра, 1800).
- Сближающиеся прямые рано или поздно пересекутся.
- Вариант: перпендикуляр и наклонная к одной и той же прямой непременно пересекаются. Утверждение известно как постулат Лежандра, хотя эта формулировка встречалась ещё в XIII веке у ат-Туси.
- Точки, равноудалённые от данной прямой (по одну её сторону), образуют прямую.
- Вариант: расстояние между параллельными прямыми всегда постоянно, то есть параллельные прямые не могут ни сближаться, ни расходиться.
- Если две прямые начали сближаться, то невозможно, чтобы они затем начали (в ту же сторону, без пересечения) расходиться (аксиома Роберта Симсона, 1756).
- Вариант: Если две прямые в одну сторону расходятся, то в другую — сближаются.
- Сумма углов одинакова у всех треугольников.
- Вариант: существует, как минимум, одна пара неравновеликих треугольников с одинаковой суммой углов.
- Существует треугольник (по меньшей мере один), сумма углов которого равна двум прямым[8].
- Две прямые, параллельные третьей, параллельны и друг другу (аксиома Остроградского, 1855).
- Линия, ортогональная некоторому семейству параллельных прямых, является прямой.
- Прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую.
- Для всякого невырожденного треугольника существует описанная окружность (аксиома Фаркаша Бойяи).
- Справедлива теорема Пифагора (как минимум в одном прямоугольном треугольнике).
- Вариант: пространство имеет Евклидову метрику.
- Отношение длины окружности к её диаметру является константой, то есть одинаково для любой окружности.
- Существует окружность (хотя бы одна), у которой отношение длины окружности к её диаметру равно числу Пи .
Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему.
Если вместо V постулата допустить, что для пары точка—прямая V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все вышеперечисленные эквивалентные утверждения неверны.
Система аксиом сферической геометрии требует изменения также и других аксиом Евклида[9].
Пятый постулат резко выделяется среди других, вполне очевидных, он больше похож на сложную, неочевидную теорему. Евклид, вероятно, сознавал это, и поэтому первые 28 предложений в «Началах» доказываются без его помощи.
«Евклиду безусловно должны были быть известны различные формы постулата о параллельных»[4]. Почему же он выбрал приведенную, сложную и громоздкую? Историки высказывали различные предположения о причинах такого выбора. В. П. Смилга полагал, что Евклид такой формулировкой указывал на то, что данная часть теории является незавершённой[10]. М. Клайн обращает внимание на то, что пятый постулат Евклида имеет локальный характер, то есть описывает событие на ограниченном участке плоскости, в то время как, например, аксиома Прокла утверждает факт параллельности, который требует рассмотрения всей бесконечной прямой[11]. Надо пояснить, что античные математики избегали использовать актуальную бесконечность; например, второй постулат Евклида утверждает не бесконечность прямой, а всего лишь то, что «прямую можно непрерывно продолжать». С точки зрения античных математиков, вышеприведенные эквиваленты постулата о параллельных могли казаться неприемлемыми: они либо ссылаются на актуальную бесконечность или (ещё не введенное) понятие измерения, либо тоже не слишком очевидны. Ещё одну версию выдвинул историк Имре Тот[12]: евклидова формулировка, возможно, была вначале (ошибочно доказанной) теоремой у кого-то из предшественников Евклида, и когда убедились, что доказать её не удаётся, статус теоремы повысили до постулата, не меняя текста формулировки.
Абсолютная геометрия[править | править вики-текст]
Если из списка аксиом исключить V постулат, то полученная система аксиом будет описывать так называемую абсолютную геометрию. В частности, первые 28 теорем «Начал» Евклида доказываются без использования V постулата и поэтому относятся к абсолютной геометрии. Для дальнейшего отметим две теоремы абсолютной геометрии:
- Параллельные прямые существуют; это следует из теорем 27 и 28 «Начал» Евклида.
- При продолжении двух прямых от точки их пересечения расстояние между ними неограниченно возрастает[13].
Попытки доказательства[править | править вики-текст]
Математики с давних времён пытались «улучшить Евклида» — либо исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы, либо заменить его другим, столь же очевидным, как другие постулаты. Надежду на достижимость этого результата поддерживало то, что IV постулат Евклида (все прямые углы равны) действительно оказался лишним — он был строго доказан как теорема и исключён из перечня аксиом[5].
За два тысячелетия было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг: оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же пятого постулата.
Прокл (V век н. э.) в «Комментарии к I книге Начал Евклида» сообщает, что такое доказательство предложил Клавдий Птолемей, критикует его доказательство и предлагает своё собственное[13]. В несколько упрощённом виде его можно описать так: пусть прямая 








Приведенное доказательство опирается на допущение, что расстояние между двумя параллельными прямыми постоянно (или, по крайней мере, ограничено). Впоследствии выяснилось, что это допущение равносильно V постулату.
Учёный I века до н. э. Посидоний предложил определить параллельные как прямые, на всём протяжении равноудалённые друг от друга. Из такого определения легко выводится пятый постулат. Однако определение Посидония некорректно: ниоткуда не следует, что линия, равноудалённая от данной прямой, есть прямая[14].
После упадка античной культуры V постулатом занялись математики стран ислама. Доказательство ал-Джаухари, ученика ал-Хорезми (IX век)[15], неявно подразумевало: если при пересечении двух прямых какой-либо третьей накрест-лежащие углы равны, то то же имеет место при пересечении тех же двух прямых любой другой. И это допущение равносильно V постулату.
Сабит ибн Курра (IX век) дал два доказательства; в первом он опирается на предположение, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. Во втором, как и Посидоний, он исходит из существования равноотстоящих прямых, причём этот факт ибн Курра пытается вывести из представления о «простом движении», т. е. о равномерном движении на фиксированном расстоянии от прямой (ему представляется очевидным, что траектория такого движения — тоже прямая)[16]. Каждое из двух упомянутых утверждений Ибн Курры эквивалентно V постулату.
Четырёхугольник Ламберта
Аналогичную ошибку сделал ибн ал-Хайсам, но он впервые рассмотрел фигуру, позже получившую название «четырёхугольник Ламберта» — четырёхугольник, у которого три внутренних угла — прямые. Он сформулировал три возможных варианта для четвёртого угла: острый, прямой, тупой. Обсуждение этих трёх гипотез, в разных вариантах, многократно возникало в позднейших исследованиях.
Поэт и математик Омар Хайям подверг критике попытки ввести в геометрию механическое движение. Он предложил заменить V постулат на другой, более простой: две сходящиеся прямые пересекаются, и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Каждая из двух частей этого утверждения равносильна постулату Евклида[17].
Ал-Абхари предложил доказательство, сходное с доказательством ал-Джаухари. Это доказательство приводит в своей книге ас-Самарканди, и ряд исследователей считал его автором самого ас-Самарканди. Доказательство исходит из верного в абсолютной геометрии утверждения о том, что для всякой прямой, пересекающей стороны данного угла, может быть построена ещё одна прямая, пересекающая стороны этого же угла и отстоящая от его вершины дальше, чем первая. Но из этого утверждения автор делает логически необоснованный вывод о том, что через всякую точку внутри данного угла можно провести прямую, пересекающую обе стороны этого угла, — и основывает на этом последнем утверждении, эквивалентном V постулату, всё дальнейшее доказательство.
Насир ад-Дин ат-Туси предложил построение, аналогичное построению Омара Хайяма[18]. Отметим, что сочинения ат-Туси стали известны Джону Валлису, и тем самым сыграли роль в развёртывании исследований по неевклидовой геометрии в Европе.
Первую в Европе известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Герсонид (он же Леви бен Гершом, XIV век). Его доказательство опиралось на утверждение о существовании прямоугольника[19].
К XVI веку относится доказательство учёного-иезуита Христофора Клавиуса. Доказательство его, как и у ибн Курры, основывалось на утверждении, что линия, равноотстоящая от прямой — тоже прямая[20].
Валлис в 1693 году в одной из своих работ воспроизводит перевод сочинения ат-Туси и предлагает эквивалентную, но более простую формулировку: существуют подобные, но не равные фигуры[21]. Клеро в своих «Началах геометрии» (1741), как и Герсонид, вместо V постулата взял его эквивалент «существует прямоугольник».
В целом можно сказать, что все перечисленные попытки принесли немалую пользу: была установлена связь между V постулатом и другими утверждениями, были отчётливо сформулированы две альтернативы V постулату — гипотезы острого и тупого угла.
Первые наброски неевклидовой геометрии[править | править вики-текст]
Глубокое исследование V постулата, основанное на совершенно оригинальном принципе, провёл в 1733 году итальянский монах-иезуит, преподаватель математики Джироламо Саккери. Он опубликовал труд под названием «Евклид, очищенный от всех пятен, или же геометрическая попытка установить самые первые начала всей геометрии». Идея Саккери состояла в том, чтобы заменить V постулат противоположным утверждением, вывести из новой системы аксиом как можно больше следствий, тем самым построив «ложную геометрию», и найти в этой геометрии противоречия или заведомо неприемлемые положения. Тогда справедливость V постулата будет доказана от противного[22].
Саккери рассматривает всё те же три гипотезы о 4-м угле четырёхугольника Ламберта. Гипотезу тупого угла он отверг сразу по формальным соображениям. Легко показать, что в этом случае вообще все прямые пересекаются, а тогда можно заключить, что V постулат Евклида справедлив — ведь он как раз и утверждает, что при некоторых условиях прямые пересекаются. Отсюда делается вывод, что «гипотеза тупого угла всегда целиком ложна, так как она сама себя разрушает»[23].
После этого Саккери переходит к опровержению «гипотезы острого угла», и здесь его исследование гораздо интереснее. Он допускает, что она верна, и, одно за другим, доказывает целый ряд следствий. Сам того не подозревая, он продвигается довольно далеко в построении геометрии Лобачевского. Многие теоремы, доказанные Саккери, выглядят интуитивно неприемлемыми, но он продолжает цепочку теорем. Наконец, Саккери доказывает, что в «ложной геометрии» любые две прямые или пересекаются, или имеют общий перпендикуляр, по обе стороны от которого они удаляются друг от друга, или же удаляются друг от друга с одной стороны и неограниченно сближаются с другой. В этом месте Саккери делает неожиданный вывод: «гипотеза острого угла совершенно ложна, так как противоречит природе прямой линии»[24].
Видимо, Саккери чувствовал необоснованность этого «доказательства», потому что исследование продолжается. Он рассматривает эквидистанту — геометрическое место точек плоскости, равноотстоящих от прямой; в отличие от своих предшественников, Саккери понимает, что в рассматриваемом случае это вовсе не прямая. Однако, вычисляя длину её дуги, Саккери допускает ошибку и приходит к реальному противоречию, после чего заканчивает исследование и с облегчением заявляет, что он «вырвал эту зловредную гипотезу с корнем». К сожалению, пионерская работа Саккери, изданная посмертно, не обратила на себя того внимания математиков, которого заслуживала, и только спустя 150 лет (1889) его соотечественник Бельтрами обнаружил этот забытый труд и оценил его историческое значение.
Во второй половине XVIII века было опубликовано более 50 работ по теории параллельных. В обзоре тех лет (Г. С. Клюгель) исследуется более 30 попыток доказать V постулат и доказывается их ошибочность. Известный немецкий математик и физик И. Г. Ламберт, с которым Клюгель переписывался, тоже заинтересовался проблемой; его «Теория параллельных линий» была издана (как и труд Саккери, посмертно) в 1786 году.
Сферическая геометрия: все прямые пересекаются
Ламберт первым обнаружил, что «геометрия тупого угла» реализуется на сфере, если под прямыми понимать большие круги. Он, как и Саккери, вывел из «гипотезы острого угла» множество следствий, причём продвинулся гораздо дальше Саккери; в частности, он обнаружил, что дополнение суммы углов треугольника до 180° пропорционально площади треугольника.
В своей книге Ламберт проницательно отметил[25]:
Мне кажется очень замечательным, что вторая гипотеза [тупого угла] оправдывается, если вместо плоских треугольников взять сферические. Я из этого почти должен был бы сделать вывод — заключение, что третья гипотеза имеет место на какой-то мнимой сфере. Во всяком случае, должна же существовать причина, почему она на плоскости далеко не так легко поддаётся опровержению, как это могло быть сделано в отношении второй гипотезы.
Геометрия на поверхности отрицательной кривизны
Ламберт не нашёл противоречия в гипотезе острого угла и пришёл к заключению, что все попытки доказать V постулат безнадёжны. Он не высказал каких-либо сомнений в ложности «геометрии острого угла», однако, судя по другому его проницательному замечанию, Ламберт размышлял о возможной физической реальности неевклидовой геометрии и о последствиях этого для науки[26]:
В этом есть что-то восхитительное, что вызывает желание, чтобы третья гипотеза была справедлива. И всё же я хотел бы <…>, чтобы это было не так, потому что это было бы сопряжено с целым рядом <…> неудобств. Тригонометрические таблицы стали бы бесконечно пространными, подобие и пропорциональность фигур не существовали бы вовсе <…>, астрономии пришлось бы плохо.
Замечательная работа Ламберта, как и книга Саккери, далеко опередила своё время и не вызвала интереса у тогдашних математиков. Та же судьба постигла «астральную геометрию» немецких математиков Ф. К. Швейкарта (1817) и Ф. А. Тауринуса (1826), по идеям близкую к построенной Ламбертом.
Тем временем попытки «смыть пятна» с Евклида продолжались (Луи Бертран, Лежандр, Семён Гурьев и другие). Лежандр дал целых три доказательства V постулата, ошибочность которых быстро показали его современники[27]. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии.
Открытие неевклидовой геометрии[править | править вики-текст]
В первой половине XIX века по пути, проложенному Саккери, пошли К. Ф. Гаусс, Я. Бойяи, Н. И. Лобачевский и Ф. К. Швайкарт. Но цель у них была уже иная — не разоблачить неевклидову геометрию как невозможную, а, наоборот, построить альтернативную геометрию и выяснить её возможную роль в реальном мире. На тот момент это была совершенно еретическая идея; никто из учёных ранее не сомневался, что физическое пространство евклидово. Интересно, что Гаусса и Лобачевского учил в молодости один и тот же учитель — Мартин Бартельс, который, впрочем, сам неевклидовой геометрией не занимался.
Первым был Швайкарт. В 1818 году он отправил Гауссу письмо с серьёзным анализом основ неевклидовой геометрии, однако воздержался от вынесения своих взглядов на публичное обсуждение. Гаусс тоже не решился опубликовать работу на эту тему, но его черновые заметки и несколько писем однозначно подтверждают глубокое понимание неевклидовой геометрии. Вот несколько характерных отрывков из писем Гаусса, где впервые в науке появляется термин «неевклидова геометрия»[28]:
Допущение, что сумма трёх углов треугольника меньше 180°, приводит к своеобразной, совершенно отличной от нашей [евклидовой] геометрии; эта геометрия совершенно последовательна, и я развил её для себя совершенно удовлетворительно; я имею возможность решить в этой геометрии любую задачу, за исключением определения некоторой постоянной[29], значение которой a priori установлено быть не может.
Чем большее значение мы придадим этой постоянной, тем ближе мы подойдем к евклидовой геометрии, а бесконечно большое её значение приводит обе системы к совпадению. Предложения этой геометрии отчасти кажутся парадоксальными и непривычному человеку даже несуразными; но при строгом и спокойном размышлении оказывается, что они не содержат ничего невозможного. Так, например, все три угла треугольника можно сделать сколь угодно малыми, если только взять достаточно большие стороны; площадь же треугольника не может превысить, даже не может достичь некоторого предела, как бы велики ни были его стороны. Все мои старания найти в этой неевклидовой геометрии противоречие или непоследовательность остались бесплодными, и единственное, что в этой системе противится нашему разуму, это то, что в пространстве, если бы эта система была справедлива, должна была бы существовать некоторая сама по себе определенная (хотя нам и неизвестная) линейная величина. Но мне кажется, что мы, кроме ничего не выражающей словесной мудрости метафизиков, знаем очень мало или даже не знаем ничего о сущности пространства. (Из письма к Тауринусу, 1824)
В 1818 году в письме к австрийскому астроному Герлингу Гаусс выразил свои опасения[30]:
Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову.
Ознакомившись с работой Лобачевского «Геометрические исследования по теории параллельных», Гаусс энергично ходатайствует об избрании русского математика иностранным членом-корреспондентом Гёттингенского королевского общества (что и произошло в 1842 году).
Лобачевский и Бойяи проявили бо́льшую смелость, чем Гаусс, и почти одновременно (Лобачевский — в докладе 1826 года и публикации 1829 года; Бойяи — в письме 1831 года и публикации 1832 года), независимо друг от друга, опубликовали изложение того, что сейчас называется геометрией Лобачевского. Лобачевский продвинулся в исследовании новой геометрии дальше всех, и она в настоящий момент носит его имя. Но главная его заслуга не в этом, а в том, что он поверил в новую геометрию и имел мужество отстаивать своё убеждение (он даже предложил экспериментально проверить V постулат, измерив сумму углов треугольника)[31].
Во вступлении к своей книге «Новые начала геометрии» Лобачевский решительно заявляет[32]:
Всем известно, что в геометрии теория параллельных до сих пор оставалась несовершенной. Напрасное старание со времён Евклида, в продолжении двух тысяч лет, заставили меня подозревать, что в самых понятиях ещё не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения.<…> Главное заключение <…> допускает существование геометрии в более обширном смысле, нежели как её представил нам первый Евклид. В этом пространном виде дал я науке название Воображаемой Геометрии, где как частный случай входит Употребительная Геометрия.
Трагическая судьба Лобачевского, подвергнутого остракизму в научном мире и служебном окружении за слишком смелые мысли, показала, что опасения Гаусса были не напрасны. Но и его борьба была не напрасна. По иронии судьбы торжество смелых идей Лобачевского обеспечил (посмертно) осторожный Гаусс. В 1860-е годы была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам русского математика. В 1868 году вышла статья Э. Бельтрами, который показал, что плоскость Лобачевского имеет постоянную отрицательную кривизну (у евклидовой плоскости кривизна нулевая, у сферы — положительная); очень быстро неевклидова геометрия приобрела легальный научный статус, хотя всё ещё рассматривалась как чисто умозрительная [33].
В конце XIX—начале XX века сначала математики (Бернхард Риман, Уильям Кингдон Клиффорд), а затем и физики (Общая теория относительности, Эйнштейн), окончательно покончили с догматом о евклидовой геометрии физического пространства.
О доказательстве независимости[править | править вики-текст]
Независимость пятого постулата означает, что его отрицание не противоречит остальным аксиомам геометрии (при условии что геометрия Евклида непротиворечива). Одновременно это означает непротиворечивость геометрии Лобачевского. На самом деле верна следующая теорема[34].
Теорема. Геометрия Лобачевского непротиворечива тогда и только тогда, когда непротиворечива евклидова геометрия.
Для доказательства этой теоремы в современной математике используются модели одной геометрии в другой. В модели для точек, прямых и других объектов первой геометрии строятся объекты в рамках второй геометрии так, что для построенных объектов выполняются аксиомы первой. Таким образом, если бы противоречие нашлось в первой системе аксиом, то оно нашлось бы и во второй.
Сложно точно указать, кто и когда доказал эту теорему.
В некотором смысле можно считать, что это было сделано уже Лобачевским. Действительно, Лобачевский заметил, что геометрия орисферы в пространстве Лобачевского является ничем иным, как Евклидовой плоскостью; таким образом, существование противоречия в евклидовой геометрии влекло бы противоречие в геометрии Лобачевского[35]. На современном языке, Лобачевский построил модель евклидовой плоскости в пространстве Лобачевского. В обратную сторону его построение шло аналитически, и непротиворечивость геометрии Лобачевского следовала из непротиворечивости вещественного анализа.
Несмотря на наличие этих инструментов, Лобачевский не формулировал саму теорему непротиворечивости. Для её строгой формулировки был необходим логический анализ оснований геометрии, сделанный позже Пашем, Гильбертом и другими[34].
Появлением концепции модели мы обязаны Бельтрами. В 1868 году он построил проективную модель, конформно-евклидову модель, а также локальную модель на так называемой псевдосфере. Бельтрами также был первым, кто увидел связь геометрии Лобачевского с дифференциальной геометрией.
Построенные Бельтрами модели были развиты позже Клейном и Пуанкаре, благодаря им построение было значительно упрощено, и также были обнаружены связи и приложения новой геометрии к проективной геометрии и комплексному анализу. Эти модели убедительно доказывают, что отрицание V постулата не противоречит остальным аксиомам геометрии; отсюда вытекает, что V постулат независим от остальных аксиом и доказать его невозможно[33].
Примечания[править | править вики-текст]
- ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
- ↑ 1 2 Каган. Лобачевский, 1948, с. 164-165.
- ↑ Смилга, 1988, с. 4.
- ↑ 1 2 История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
- ↑ 1 2 Мордухай-Болтовской Д. Д. Комментарии к «Началам» Евклида, книги I-VI. Указ. соч. — С. 241-244.
- ↑ Euclid’s Fifth Postulate
- ↑ Каган. Лобачевский, 1948, с. 167-175.
- ↑ 1 2 3 Лелон-Ферран Ж., 1989, с. 255-256.
- ↑ Joel Castellanos. Non-Euclid. Axioms and Theorems (англ.). Проверено 11 февраля 2010. Архивировано из первоисточника 19 августа 2011.
- ↑ Смилга, 1988, с. 59-61.
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 169.
- ↑ Tóth I. Das Parallelenproblem im Corpus Aristotelicum // Archive for history of exact sciences. — Berlin—Heidelberg—New York, 1967. — Т. 3, вып. 4,5. — С. 249-422.
- ↑ 1 2 Смилга, 1988, с. 72.
- ↑ Лаптев Б. Л. Н. И. Лобачевский и его геометрия. — М.: Просвещение, 1976. — С. 71. — 112 с.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
- ↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и примечания Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
- ↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М., 1962.
- ↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, примечания Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
- ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
- ↑ Clavius C. Euclidis Elementorum, libri XV. — Romae, 1574.
- ↑ Wallis. Opera mathematica, v. II. — Oxoniae, 1693. — С. 665.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 100.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 105.
- ↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin, 1781—1784. — С. 202—203.
- ↑ Смилга, 1988, с. 121.
- ↑ История математики, том III, стр. 218.
- ↑ Об основаниях геометрии, стр. 101-120.
- ↑ Из другого письма следует, что постоянная равна
, где
обозначает кривизну.
- ↑ Об основаниях геометрии, с. 119—120.
- ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949.
- ↑ Об основаниях геометрии, с. 61-62.
- ↑ 1 2 Arcozzi, Nicola. Beltrami’s models of non-euclidean geometry (англ.). Проверено 16 июля 2016.
- ↑ 1 2 Погорелов А. В. Основания геометрии. — Изд. 4-е. — М.: Наука, 1979. — С. 18—21. — 152 с.
- ↑ смотри пункт 34 в Lobachevsky, N. I. Geometrische Untersuchungen zur Theorie der Parallellinien. — Berlin: F. Fincke, 1840.
Литература[править | править вики-текст]
- Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948.
- Текст книг I—VI на www.math.ru или на mccme.ru
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Гильберт Д. Основания геометрии. — Л.: Сеятель, 1923. — 152 с.
- История математики с древнейших времён до начала XIX столетия. — М.: Наука, 1972.
- Каган В. Ф. Геометрия Лобачевского и её предыстория. — М.—Л., 1949.
- Каган В. Ф. Лобачевский. — Издание второе, дополненное. — М.-Л.: АН СССР, 1948. — 507 с.
- Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — 312 с. — ISBN 5-03-001008-4.
- Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М., 1956.
- Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. — М.: Наука, 1976.
- Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. — М.: Наука, 1983.
- Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. — 2-е изд. — М.: Молодая гвардия, 1988. — 288 с. — (Эврика).
- Успенский В. А. Апология математики. Глава 8. Параллельные прямые — в мифологии, реальности и математике. — М.: Амфора, 2009. — ISBN 978-5-367-00689-6.
Ссылки[править | править вики-текст]
| Аксиома параллельности Евклида на Викискладе? |
- Александров А. Д. Тупость и гений. «Квант», №№ 11, 12 (1982). Проверено 9 октября 2009. Архивировано из первоисточника 19 августа 2011.
- Возникновение неевклидовой геометрии. Проверено 9 октября 2009. Архивировано из первоисточника 19 августа 2011.
- Пятый постулат Евклида. Проверено 9 октября 2009. Архивировано из первоисточника 21 августа 2011.