Слайд 2Қосу формулалары
9 сынып
Мұғалім: Пирниязова Р.М.
Алгебра:тригонометрия бөлімі

Слайд 3Сабақтың мақсаты
білімділік : екі бұрыштың қосындысы мен айырымындағы тригонометриялық функциялардың формулалары
туралы түсінік беру; осы формулаларды тригонометриялық функцияларды тепе-тең түрлендіруде қолдануды үйрету.
дамытушылық : оқушылардың өз бетінше жұмыс істей білу, өз жұмысын бағалай білу дағдысын, логикалық ойлау қабілетін дамыту.
тәрбиелік:өз жұмысына жауапкершілікпен қарауға, жүйелі түрде жұмыс істеуге, өз ойын дәл, тиянақты айта білуге үйрету.

Слайд 41. Ұйымдастыру кезеңі:
Бүгінгі сабақта өз білімдеріңді өздерін бағалап отырасыңдар. Ол
үшін сіздерге «Сәттілік» картасы қажет болады. Оған аты-жөндеріңді жазасыздар.Парақта бүгінгі сабақтың тапсырмалары келтірілген. Әрбір дұрыс орындалған тапсырманың тұсына «плюс» таңбасын қойып отырасыздар. Сабақ соңында әр оқушы өз жинаған «плюс»-тарын санап, өз білімін бағалай алады. Әрине бұл жұмыс шындықты, жауапкершілікті талап етеді. Мен сіздердің шыншыл адам екендеріне сенемін. Ал енді сабағымызды бастайық.

Слайд 5Тригонометриялық функциялардың таңбалары
“Білім алудың негізі – қайталау”
(халық даналығы)
2. Үй жұмысын тексеру.

Слайд 6Тригонометриялық функциялардың жұп немесе тақтығы
sin тақ функция, сондықтан «-» таңбасы функция
алдына шығады
cos жұп функция, сондықтан «-» таңбасы жойылып кетеді
tg тақ функция, сондықтан «-» таңбасы функция алдына шығады
сtg тақ функция, сондықтан «-» таңбасы функция алдына шығады

Слайд 7Қайталау есептері «Сәттілік» картасында
1) Берілген бұрыштар қай ширекке тиісті:
а)
36°; б) 340°; в) -270° г) -125°
2) Берілген функцияның таңбасы қандай:
а) cos 280 ° б) sin 179° ;
в) tq 500° г) ctq 359°
3) Берілген функцияның жұп немесе тақтығын анықтаңдар
а) sin ( -α ) б) cos ( — α );
в) tq ( — α ) г) ctq ( — α )

Слайд 8Тригонометриялық формулаларды
қайталау
«Тригонометрия элементтері» тарауын өту барысында тригонометриялық формулалардың әртүрлі
топтарымен және осы формулаларды өрнектерді түрлендіруде қолданумен таныстыңдар.
Кім осы топтарды атап өте алады?
Негізгі тригонометриялық тепе-теңдіктер
Келтіру формулалары.

Слайд 12
Ал енді бүгінгі сабақта тригонометриялық формулалардың тағы бір тобымен танысасыздар: бұл
— қосу формулалары деп аталатын топ

Слайд 13Жаңа тақырып:
Қосу формулалары
“Барлық істің басшысы – білім мен ұғым” (Конфуций)

Слайд 14cos ( α +β) =cosα cos β – sinα sinβ
сos
(α — β) =cosα cosβ + sinα sinβ
sin (α +β) =sinα cosβ + cosα sinβ
sin (α –β )=sinα cosβ – cosα sinβ
Қосу формулалары

Слайд 16Мысалы: cos105° бұрышының мәнін есептеңдер
Осы сияқты sin105°, tg105°, ctg105° мәндерін
есептеуге болады

Слайд 17 Деңгейлік
тапсырмалар
«Бар нәрсеге қолды жеткізер — білім»

Слайд 18ІІІ деңгей тапсырмасы :
1) 75°-ты 45°+30°арқылы өрнектеп, sin75° және cos75°
мәндерін есептеңдер
2) 15°-ты 45°-30°арқылы өрнектеп, sin15° және cos15° мәндерін есептеңдер

Слайд 19ІІ деңгей тапсырмасы
Өрнектің мәнін табыңдар:
1) сos107°cos17°+sin107°sin17°
2) sin63°cos27°+cos63°sin27°
3) sin51°cos21°- cos51°sin21°

Слайд 20І деңгей тапсырмасы
1)Егер
және
болса, онда
-ны
есептеңдер;
2)Егер
және
болса, онда
-ны есептеңдер;
және
І-ширекте
және
І-ширекте
3)Егер
және
-оң сүйір бұрыштар және
болса,онда
-ны табыңдар

Слайд 211
2
3
4
5
6
«Білімді мыңды жығады, …»
(МАБ – 2011 тест тапсырмалары)

Слайд 221 – нұсқа 27 есеп
Өрнектің мәнін табыңдар:
1) сos40°cos20°-sin40°sin20°

Слайд 237 – нұсқа 27 есеп
Өрнекті ықшамдаңыз:

Слайд 2713 – нұсқа 27 есеп
және олар І-ширекте
болса, онда
өрнегінің

Слайд 28«Білім теңіз түбі
де, шегі де жоқ»

Слайд 29Қорытынды:
Сонымен бүгінгі сабақта біз не үйрендік? Қандай формулалармен таныстық?
Енді бүгінгі сабақты
қорытындылау үшін келесі сәйкестендіру тестін орындайық.

Слайд 31Енді жалпы тригонометрия тарауын өту барысында қандай формулалар- мен таныстық, қандай
жаңа ұғымдармен таныстық осыны топтастыру арқылы келтірейік.

Слайд 32Тригонометрия
тарауында не
үйрендік?
Тригонометрия-
лық функция-
лардың таңбалары
Негізгі тригоно-
метриялық тепе-
теңдіктер
Қосу
формулалары
Келтіру
формулалары
Тригонометрия-
лық функция-
лардың жұп

Слайд 33Үйге тапсырма: п.22,
№346 есеп және
тригонометрияның шығу
тарихы туралы реферат
жазып
келу

1.6_9 сынып __Қосу формуласы Презентация.pptx
Тригонометриялық функциялардың аргументі дегенді қалай түсінесіз?
1. Тригонометриялық функциялардың аргументі дегенді қалай түсінесіз? Мысал келтіріңіз.
2. Аргументтер қандай әріптермен белгіленеді?
3. Тригонометриялық функциялардың аргументтерінің қосындысы қалай жазылады?
4. Тригонометриялық функциялардың аргументтерінің айырмасы қалай жазылады?
5. Бүгінгі сабақтың тақырыбы мен мақсаты қандай деп ойлайсыз?
Сабақ тақырыбы: Қосу формулалары
Сабақ тақырыбы:
Қосу формулалары
Сабақтың мақсаты:
Аргументтің қосынысы мен айырмасының тригонометриялық формуласын қорытып шығарады және қолданады
Қосу формулалары
Қосу формулалары
Екі бұрыштың айырмасының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің қосындысына тең
1)Екі бұрыштың айырмасының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің қосындысына тең.
Екі бұрыштың қосындысының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің айырымына тең
2) Екі бұрыштың қосындысының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің айырымына тең.
Екі бұрыштың қосындысының синусы осы бұрыштардың синустары мен косинустарының көбейтінділерінің қосындысына тең
3) Екі бұрыштың қосындысының синусы осы бұрыштардың синустары мен косинустарының көбейтінділерінің қосындысына тең
Екі бұрыштың айырмасының синусы осы бұрыштардың синустары мен косинустарының көбейтінділерінің айырмасына тең
4) Екі бұрыштың айырмасының синусы осы бұрыштардың синустары мен косинустарының көбейтінділерінің айырмасына тең.
1.6_9 сынып __Қосу формуласы Презентация
1.6_9 сынып __Қосу формуласы Презентация
1.6_9 сынып __Қосу формуласы Презентация
Ауызша есеп:
Ауызша есеп:
Рефлексия Рефлекция. Аяқталмаған сөйлем
Рефлексия
Рефлекция.
Аяқталмаған сөйлем
Мен білетін едім…………..
Мен бүгін білдім…………..
Білгім келетіні…………..
Маған ұнады………………….
Маған ұнамады……………
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email
Поделитесь с коллегами:
Күні:
Сыныбы: 9Ә
Тақырыбы: Қосу формулалары
Мақсаты: Қосу формулалары туралы түсінік беріп, екі бұрыштың қосындысы мен айырымының формулаларын қорытып шығару жолдарын үйрету; қосу формулаларын есептер шешуде қолдану икемдігін қалыптастыру; Оқушылардың есте сақтау қабілеттерін дамыту. Оқушыларды ұқыптылыққа, шапшаңдыққа тәрбиелеу.
Сабақтың әдісі: түсінік беру, сұрақ-жауап
Сабақтың түрі: жаңа материалды меңгерту
Сабақтың барысы:
І. Ұйымдастыру бөлімі
Оқушылармен амандасу, түгелдеу. Оқушылардың сабаққа дайындығын
тесеріп, олардың көңілдерін сабаққа аудару.
ІІ. Үй тапсырмасын тексеру бөлімі
Тригонометриялық функцияларды атаңдар.
Қандай функциялар жұп, қандай функциялар тақ болады?
Келтіру формулаларын жазып беріңдер.
ІІІ. Жаңа сабаққа әзірлік
-
sin α, cos α, tg α, ctg α функцияларының анықтамасын, олардың жұп немесе тақ екенін еске түсіру.
-
Екі вектордың арасындағы бұрыш дегеніміз не?
-
Вектордың скалярлық көбейтіндісі деген не?
ІҮ. Жаңа сабақ материалын түсіндіру
Қосу формулалары.
Анықтама. Екі бұрыштың қосындысы мен айырымының тригонометриялық
функцияларын сол бұрыштардың тригонометриялық функциялары арқылы
өрнектейтін формулаларды қосу формулалары деп атайды.
Теорема. Кез келген α; β бұрыштары үшін
cos(α — β)=cosα cosβ + sinα sinβ (1)
Радиусы r-ге тең шеңбердің ОА радиусын оның центрі О нүктесінен
айналдыра β және α бұрыштарына бұрайық. Сонда ОА радиусы сәйкесінше
ОВ және ОС радиусына көшеді.



С(х2;у2) В(х1;у1) ОВ мен ОС векторларының скалярлық

А х ОВ * ОС =х1х2+у1у2 (*)
формуласымен анықталатынын геометрия
к
Осыларды (*) теңдігіне қойсақ, ОВ *ОС = r cos α r cos β+ r sin α r sin β, бұдан
О
Екінші жағынан скалярлық көбейтіндінің анықтамасы бойынша:
О

cos(α — β)=cosα cosβ + sinα sinβ (1)
Екі бұрыштың айырымының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің қосындысына тең.
cos(α + β)=cosα cosβ — sinα sinβ (2)
Екі бұрыштың қосындысының косинусы осы бұрыштардың косинустарының көбейтіндісі мен синустарының көбейтіндісінің айырымына тең.
Келтіру формулаларын қолдансақ:
sin (α + β)= sinα cosβ + cosα sinβ (3)
Екі бұрыштың қосындысының синусы бірінші бұрыштың синусы мен екінші бұрыштың косинусының көбейтіндісіне бірінші бұрыштың косинусы мен екінші бұрыштың синусы көбейтіндісін қосқанға тең.
sin (α — β)= sinα cosβ — cosα sinβ (4)
екі бұрыштың айырымының синусы бірінші бұрыштың синусының екінші бұрыштың косинусына көбейтіндісі мен бірінші бұрыштың косинусының екінші бұрыштың синусына көбейтіндісінің айырымына тең.
tg (α+β)=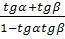
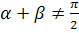
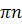
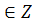
tg (α — β)=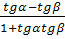
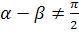
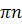
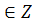
ctg(α + β)= 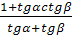
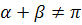
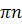
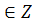
ctg(α — β)= 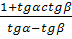
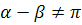
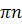
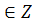
(1)- (8) формулалары қосу формулалары деп аталады.
Ү. Есептер шығару.
Оқулықпен жұмыс.
№ 498.
-
cos (
= cos
cosα — sin
sinα =
cosα —
sinα
-
sin(
= sin
cosα — cos
sinα =
cosα —
sinα
№ 499.
1. sin1500= sin(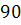
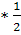
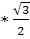

2.cos1500= cos(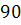
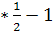
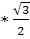
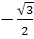
№ 501.
cos1030 cos130 + sin1030 sinβ130 =cos(1030 — 130)=cos 900 =0
cos150 cos300 — sin300 sinβ150 =cos(150 + 300)=cos 450 =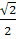
sin510 cos390 + cos510 sin390=sin(510+390)=sin900=1
sin630 cos330 — cos630 sin330=sin(630+330)=sin300=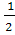
ҮІ. Сабақты бекіту
-
Екі бұрыштың қосындысы мен айырымының синусы, косинусы формулалары қалай дәлелденеді?
-
Екі бұрыштың айырымы мен қосындысының тангенсі мен котангенсі неге тең?
ҮІІ . Үйге тапсырма
№502. Түсіндіру.
ҮІІІ. Бағалау
Оқушыларды бағалап, жетістіктерін айтып, мадақтау, кемшіліктерін ескерту.
ІХ. Қорытынды.
Сабақ аяқталды. Сау болыңыздар.

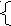
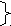




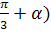 = cos
= cos cosα — sin
cosα — sin 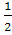 cosα —
cosα —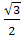 sinα
sinα 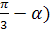 = sin
= sin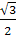 cosα —
cosα —