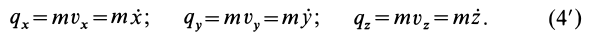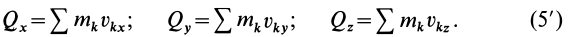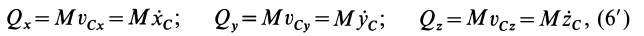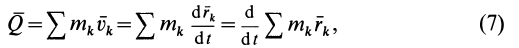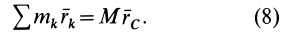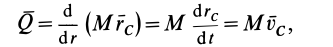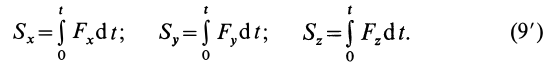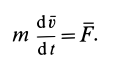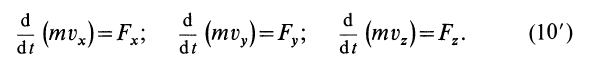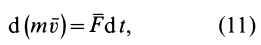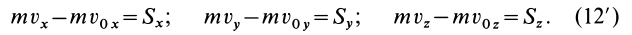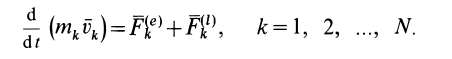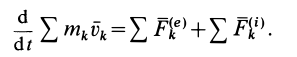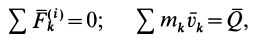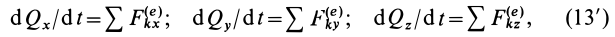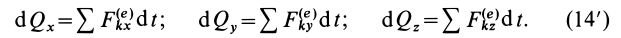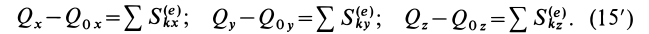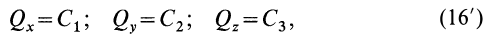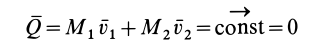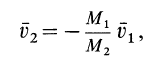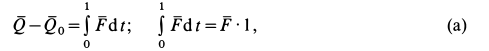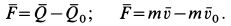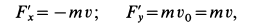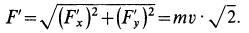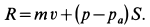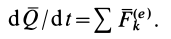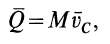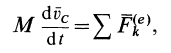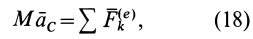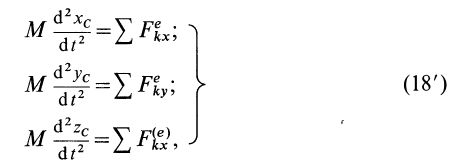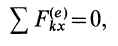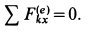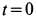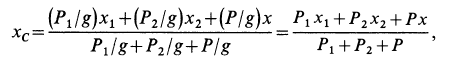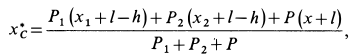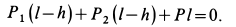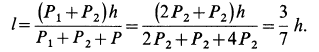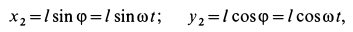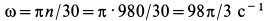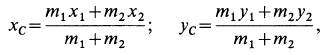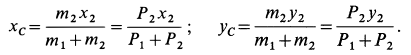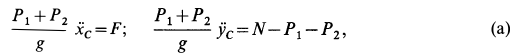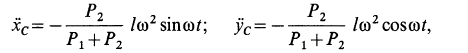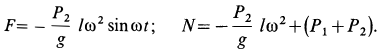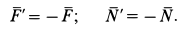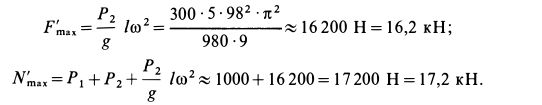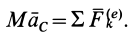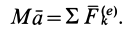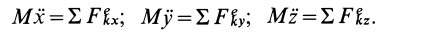Количество
движения материальной точки— вектор,
численно равный произведению массы
точки на скорость ее движения и совпадающий
с ней по направлению.
Векторная
производная по времени от количества
движения материальной точки геометрически
равна вектору силы, действующей на
точку.
Основное
уравнение динамики:
;
.
Интегрируя получим :
.-импульс
силы.
Импульс
силы— векторная величина, характеризующая
передачу материальной точке механического
движения за некоторый промежуток времени
со стороны других тел, действующих на
нее, равна произведению силы на время
ее действия и совпадает с ней по
направлению:;
В проекциях на оси:
34)Теорема об изменении количества движения точки(на всякий случай кинул и момента) и системы.
Теорема:
Изменение количества движения материальной
точки за некоторый промежуток времени
равно импульсу силы, действующей на
точку за этот промежуток времени.
Основное
уравнение динамики:
;
.
Интегрируя получим :
.-импульс
силы.
(((((теорема
об изменении момента кол движ:
;
взяв производную по времени от обоих
частей уравнения получим:
,
итак:.
Теорема:
векторная производная по времени от
момента количества движения материальной
точки относительно полюса равна вектору
момента силы, действующей на точку
относительно того же центра.
Следствия:
1.
если линия действия силы проходит через
полюс. То момент количества движения
относительно этого полюса постоянный;
2.
если момент силы относительно оси равен
нулю, то момент количества движения
относительно этой оси постоянный.))))))
Количество
движения механической системы— вектор,
равный геометрической сумме всех
количеств движения материальных точек
этой системы, численно равный произведению
массы системы на скорость центра масс
и совпадающий с ней по направлению.
Векторная
производная по времени от количества
движения механической системы
геометрически равна главному вектору
внешних сил, действующих на механическую
систему.
.
Так как:
,
то:;
интегрируя получим:
.
Теорема:
Изменение количества движения механической
системы за некоторый промежуток времени
равно геометрической сумме импульсов
внешних сил, действующих на систему за
этот промежуток времени.
Следствия:
1.
внутренние силы не влияют на изменение
количества движения;
2.
Закон сохранения количества движения
механической системы: если главные
векторы всех внешних сил, действующих
на точки системы, равны нулю, то вектор
количества движения механической
системы остается постоянным.
3.
Закон сохранения проекции вектора
количества движения механической
системы: если проекции векторов всех
внешних сил, действующих на точки
системы, на ось равны нулю, то проекция
вектора количества движения механической
системы на эту ось остается постоянной.
35)Работа силы и момента силы. Мощность
Работа
силы—
количественная мера превращения
механического движения в другие виды
движения.
Если
сила постоянна по модулю и направлению,
а точка ее приложения перемещается
прямолинейно, то работа равна произведению
модуля силы, длинны перемещения и
косинуса угла между этими векторами:
.Знакработы
совпадает со знаком проекции силы на
ось перемещения..
Интегрируя для точки М получим:
Мощность—
работа, выполненная за единицу времени.
Теорема
о работе равнодействующей силы:
работа равнодействующей на некотором
перемещении равна алгебраической сумме
работ, составляющих ее сил на этом же
перемещении.
Работа
сил тяжести, упругости.Работа
силы тяжестичисленно
равна произведению силы тяжести на
вертикальное перемещение точки ее
приложения, не зависит от траектории
перемещения, а только от расстояние
между вертикальными проекциями начального
и конечного положения точки:
Работа
силы упругостичисленно
равна произведению половины коэффициента
жесткости на квадрат перемещения точки
приложения силы, поскольку модуль силы
упругости равен произведению коэффициента
жесткости на удлинение:
.
Работа
сил, приложенных к твердому телу.Работа
внутренних сил на конечном перемещении
равна нулю.
Работа
силы, действующей на поступательно
движущееся тело равна произведению
этой силы на приращение линейного
перемещения.
Работа
силы, действующей на вращающееся тело
равна произведению момента этой силы
относительно оси вращения на приращение
угла поворота:
;
.
Мощность:.
Работа
момента силы — это мера воздействия
момента силы на тело на данном пути (во
вращательном движении). Она равна
произведению модуля момента силы и угла
поворота.
Понятие
работы представляет собой меру внешних
воздействий, приложенных к телу на
определенном пути, вызывающих изменения
механического состояния тела.
Содержание:
Количество движения точки и системы:
Одной из мер движения точки или системы является количество их движения.
Количеством движения материальной точки
Количество движения точки в физике часто называют импульсом материальной точки.
Проекции количества движения точки на прямоугольные декартовы оси координат:
Размерность количества движений в СИ — 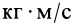
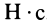
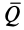
и, следовательно, проекции количества движения системы на прямоугольные декартовы оси координат
Вектор количества движения системы 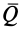
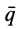
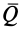
Вычисление количества движения системы
Количество движения системы можно выразить через массу системы 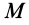
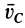
В проекциях на прямоугольные декартовы оси соответственно
где 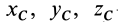
где 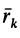
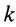
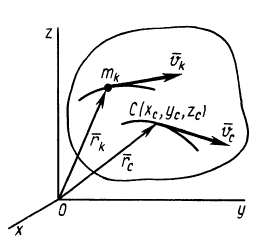
Рис. 40
По формуле для радиуса-вектора центра масс,
Подставляя значение статического момента массы (8) в (7), имеем
так как масса системы 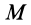
Элементарный и полный импульсы силы
Действие силы 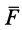
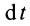
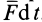
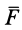
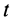
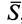
Проекции импульса силы на прямоугольные оси координат выражаются формулами
Единица импульса силы — 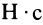
Теорема об изменении количества движения точки
Дифференциальное уравнение движения материальной точки под действием силы 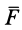
Так как масса точки 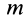
Формула (10) выражает теорему об изменении количества движения точки в дифференциальной форме: первая производная по времени от количества движения точки равна действующей на точку силе.
В проекциях на координатные оси (10) можно представить в виде
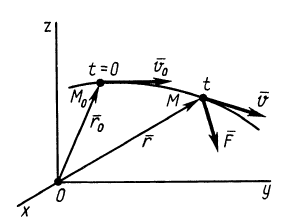
Рис. 41
Если обе части (10) умножить на 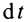
т. е. дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Проецируя обе части (11) на координатные оси, получаем
Интегрируя обе части (11) в пределах от нуля до 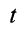
где 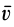
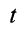
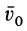
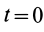
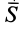
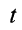
Выражение в форме (12) часто называют теоремой импульсов в конечной (или интегральной) форме: изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за тот же промежуток времени. В проекциях на координатные оси эту теорему можно представить в следующем виде:
Для материальной точки теорема об изменении количества движения в любой из форм, по существу, не отличается от дифференциальных уравнений движения точки.
Теорема об изменении количества движения системы
Аналогично тому, как для одной материальной точки, выведем теорему об изменении количества движения для системы в различных формах. Пусть к точкам системы приложены внешняя и внутренняя силы. Тогда для каждой точки можно применить теорему об изменении количества движения, например в форме (10) (см. рис. 40):
Суммируя по всем точкам системы правые и левые части этих соотношений и учитывая, что сумма производных равна производной от суммы, получаем
Так как, по свойству внутренних сил и определению количества движения системы,
то приведенное соотношение можно представить в виде
Выражение (13) является теоремой об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна векторной сумме всех внешних сил, действующих на систему. В проекциях на прямоугольные декартовы оси координат
т. е. производная по времени от проекции количества движения системы на какую-либо координатную ось равна сумме проекций всех внешних сил системы на ту же ось.
Умножая обе части (13) на 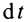
т. е. дифференциал количества движения системы равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему. В проекциях на координатные оси эта теорема примет вид
Вычисляя интегралы от обеих частей (14) по времени- от нуля до получаем теорему импульсов для системы в конечной или интегральной форме:
где 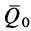
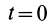
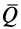
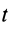
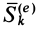
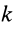
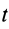
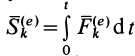
Теорема импульсов для системы в конечной форме формулируется так: изменение количества движения системы за какое-либо время равно векторной сумме всех импульсов внешних сил, действующих на систему за то же время. В проекциях на прямоугольные оси согласно (15) имеем:
Внутренние силы системы не входят явно в теорему об изменении количества движения системы в любой из форм и, следовательно, не влияют непосредственно на изменение количества движения системы. Они могут влиять на изменение количества движения только неявно через внешние силы.
Из теоремы об изменении количества движения для точки и системы при некоторых условиях для внешних сил можно получить так называемые первые интегралы системы дифференциальных уравнений точки и системы. Эти первые интегралы называют законами сохранения количества движения или проекции количества движения на ось. Рассмотрим эти законы сохранения для точки и системы одновременно, считая материальную точку механической системой, состоящей из одной точки.
Законы сохранения количества движения
Законы сохранения количества движения системы получаются как частные случаи теоремы об изменении количества движения для системы в зависимости от особенностей системы внешних сил, приложенных к рассматриваемой механической системе, а для одной точки — от особенностей сил, действующих на точку. Внутренние силы при этом могут быть любыми, так как они явно не влияют на изменение количества движения системы.
Возможны два частных случая.
1. Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, т. е. 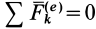
Этот закон (точнее, частный случай теоремы) формулируется так: если главный вектор внешних сил системы равен нулю, то количество движения системы постоянно по величине и направлению. В проекциях на координатные оси, по этому закону,
где 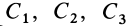
В соотношения (16) и (16′) входят производные от координат точек по времени не выше первого порядка и не входят вторые производные от этих координат. Следовательно, эти соотношения являются первыми интегралами дифференциальных уравнений системы (3).
2. Если равна нулю проекция главного вектора внешних сил на какую-либо координатную ось 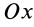
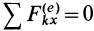
Выражение (17) является законом сохранения проекции количества движения системы: если проекция главного вектора всех внешних сил системы на какую-либо ось равна нулю, то проекция количества движения на ту же ось является постоянной величиной.
Применим закон сохранения количества движения системы для объяснения принципа реактивного движения. Пусть, например, система состоит из двух сочлененных твердых тел, находящихся в покое и свободных от действия внешних сил. Тогда для рассматриваемой системы количество движения все время постоянно и равно нулю. Допустим, что при взрыве пиропатрона (действие внутренних сил) первому телу массой 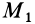
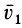
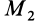
Следовательно,
т. е. второе тело движется в сторону, противоположную первому телу. Если его движению препятствует какая-либо связь, то рассматриваемое тело давит на эту связь с некоторой силой по направлению скорости 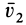
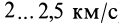
Теорему об изменении количества движения в той или другой форме удобно применять для решения задач именно в рассмотренных частных случаях, хотя в некоторых случаях ее применяют и в общем случае. Отметим, что внутренние силы не влияют на изменение количества движения в изолированных системах, т. е. в системах, которые не соприкасаются с другими телами, не принадлежащими к рассматриваемой системе, или окружающей систему материальной средой.
В неизолированных механических системах внутренние силы, вызывая движение отдельных частей системы вследствие взаимодействия с внешними телами или окружающей материальной средой, могут вызвать внешние силы в виде сил реакций связей или изменения активных сил, которые могут изменить количество движения системы.
Количество движения системы может зависеть от внутренних сил только неявно, через внешние силы.
Рис. 42
Пример №1
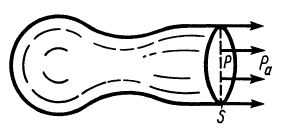
Через изогнутую под прямым углом трубу постоянного сечения за 1 с протекает жидкость массой 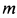
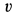
Решение:
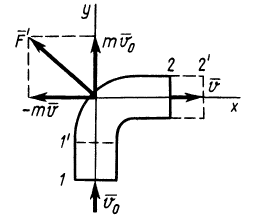
Применим к объему жидкости, заключенному между стенками трубы и поперечными сечениями 1 и 2, теорему об изменении количества движения в форме теоремы импульсов за промежуток времени, равный 1 с. За секунду точки жидкости из сечения 1 сместятся на расстояние 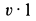
где 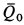
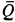
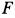
Так как в общей части объема жидкости количества движения, входящие в 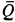
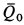
Сила давления жидкости 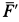
Проецируя (б) на оси координат, получаем
так как 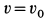
Направление силы давления жидкости 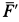
Рис. 43
Если бы через сечение 1 жидкость не поступала, а образовывалась внутри трубы, как в реактивном двигателе образуются газы после сгорания топлива, а через сечение 2 она выходила (рис. 43), то сила 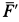
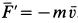
Эта сила 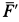
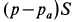
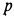
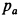
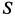
Полная реактивная сила двигателя
По направлению реактивная сила 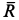
- Заказать решение задач по теоретической механике
Теорема о движении центра масс системы
Следствием теоремы об изменении количества движения системы является теорема о движении центра масс системы. По теореме об изменении количества движения системы (13),
Но количество движения системы можно вычислить по формуле (6):
где 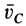
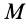
Подставляя (6) в (13) и учитывая, что масса системы постоянна, получаем теорему о движении центра масс в векторной форме:
или
где 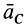
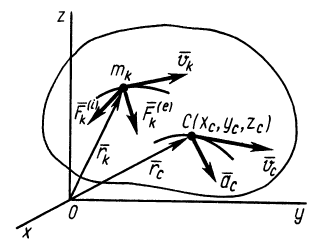
Рис. 44
Теорема о движении центра масс формулируется так: центр масс системы движется так же, как и материальная точка, масса которой равна массе всей системы, если на точку действуют все внешние силы, приложенные к рассматриваемой механической системе.
Проецируя (18) на прямоугольные декартовы оси координат (рис. 44), получаем дифференциальные уравнения движения центра масс:
где 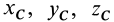
Из теоремы о движении центра масс можно получить следствия, аналогичные законам сохранения количества движения и проекции количества движения на ось.
1. Если главный вектор внешних сил, действующих на систему, равен нулю, т. е. 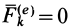
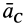
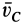
2. Если проекция, например на ось 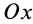
то из (18′) следует, что проекция ускорения 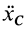
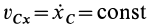
Рис. 45
Если дополнительно в начальный момент 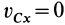
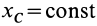
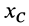
Внутренние силы не влияют явно на движение центра масс. Они могут влиять только неявно, через внешние силы. Следовательно, одними внутренними силами, без внешних, нельзя вывести из равновесия или изменить движение центра масс системы. Но внутренними силами для неизолированной механической системы можно создать движение отдельных частей системы и, следовательно, взаимодействие с внешними телами, вызывая этим внешние силы реакций связей или изменяя активные силы. Это может изменить движение центра масс или вывести его из равновесия.
Пусть человек стоит на абсолютно гладкой горизонтальной плоскости вблизи скрепленного с этой плоскостью тела. Так как на человека не действуют внешние силы в горизонтальном направлении, то внутренними силами он не может вывести из равновесия в этом направлении свой центр масс. Но человек может оттолкнуться рукой от препятствия, т. е. внутренними силами вызвать внешнюю силу реакций препятствия и таким образом вызвать движение своего центра масс в горизонтальном направлении. Все, что движется по Земле, летает в воздухе, плавает по воде, совершает это с помощью внутренних сил, создавая внешние силы трения на твердых поверхностях внешних тел, отталкиваясь от воздуха или воды.
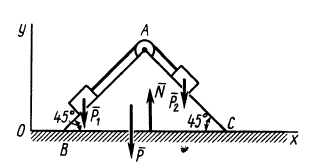
Пример №2
Два груза с силами тяжести 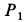
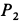
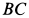
Найти перемещение клина по плоскости при опускании груза 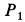
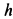
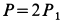
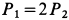
Решение:
Внешними силами, действующими на клин вместе с грузами, являются силы тяжести 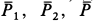
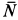
Учитывая, что в начальный момент система находится в покое, на основании второго следствия из теоремы о движении центра масс имеем 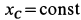
Вычислим 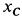
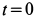
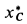
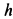
Для момента
где 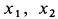
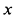
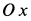
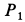
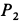
Пусть вся система вместе с клином переместилась в положительном направлении оси 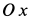
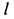
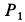
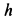
так как грузы вместе с клином передвинутся на 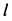
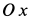
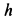
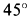
Так как 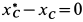
Отсюда
Так как величина 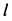
Рис. 46
Пример №3
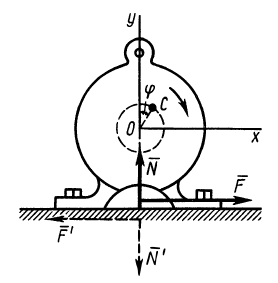
В электромоторе корпус (статор) имеет силу тяжести 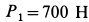
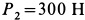
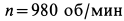
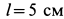
Определить горизонтальную силу, с которой действует мотор на болты, крепящие его к фундаменту, и вертикальное давление на пол.
Решение:
Предположим, что при 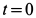
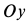
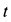
где
Для определения давления мотора на болты и пол рассмотрим в качестве механической системы весь мотор, для которого внешней силой в горизонтальном направлении является только сила действия болтов 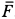
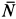
где 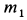
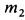
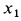
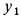
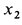
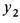
Центр масс корпуса закрепленного мотора является неподвижной точкой и находится в начале координат. Следовательно, 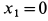
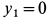
Используя дифференциальные уравнения движения центра масс всего мотора в проекциях на координатные оси, получим
где 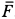
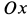
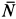
то из (а) следует
Сила действия мотора на болты 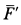
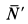
Наибольшие числовые значения этих сил
Если болтов нет, то корпус мотора может подпрыгивать в направлении оси 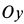
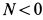
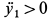
Дифференциальные уравнения поступательного движения твердого тела
Из теоремы о движении центра масс системы получаются дифференциальные уравнения поступательного движения твердого тела. Имеем
Но при поступательном движении твердого тела ускорения всех точек тела одинаковы по модулю и направлению, т. е. 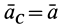
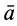
Проецируя на оси координат, имеем:
Это и есть дифференциальные уравнения поступательного движения твердого тела в проекциях на прямоугольные оси координат. В этих уравнениях х, у, z являются координатами произвольной точки тела, в частности могут быть координатами его центра масс. Тело, совершающее поступательное движение, имеет три степени свободы, и поэтому можно составить три дифференциальных уравнения его движения.
Дифференциальные уравнения поступательного движения твердого тела аналогичны дифференциальным уравнениям движения одной материальной точки. С помощью этих уравнений можно решать такие же задачи, как и для одной точки.
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Закон сохранения механической энергии
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
Количество движения материальной точки – векторная величина, равная произведению массы точки на вектор ее скорости.
Единицей измерения количества движения является (кг м/с).
Количество движения механической системы – векторная величина, равная геометрической сумме (главному вектору) количества движения механической системы равняется произведению массы всей системы на скорость ее центра масс.
Когда тело (или система) движется так, что ее центр масс неподвижен, то количество движения тела равняется нулю (например, вращение тела вокруг неподвижной оси, проходящей через центр масс тела).
В случае сложного движения, количество движения системы не будет характеризовать вращательную часть движения при вращении вокруг центра масс. Т.е., количество движения характеризует только поступательное движение системы (вместе с центром масс).
Импульс силы
Импульс силы характеризует действие силы за некоторый промежуток времени.
Импульс силы за конечный промежуток времени определяется как интегральная сумма соответствующих элементарных импульсов.
Теорема об изменении количества движения материальной точки
(в дифференциальной форме):
Производная по времени от количества движения материальной точки равна геометрической сумме действующих на точки сил.
(в интегральной форме):
Изменение количества движения материальной точки за некоторый промежуток времени равняется геометрической сумме импульсов сил, приложенных к точке за этот промежуток времени.
Теорема об изменении количества движения механической системы
(в дифференциальной форме):
Производная по времени от количества движения системы равна геометрической сумме всех внешних сил, действующих на систему.
(в интегральной форме):
Изменение количества движения системы за некоторый промежуток времени равняется геометрической сумме импульсов внешних сил, действующих на систему за этот промежуток времени.
Теорема позволяет исключить из рассмотрения заведомо неизвестные внутренние силы.
Теорема об изменении количества движения механической системы и теорема о движении центра масс являются двумя разными формами одной теоремы.
Закон сохранения количества движения системы
- Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным по направлению и по модулю.
- Если сумма проекций всех действующих внешних сил на любую произвольную ось равна нулю, то проекция количества движения на эту ось является величиной постоянной.
Выводы:
- Законы сохранения свидетельствуют, что внутренние силы не могут изменить суммарное количество движения системы.
- Теорема об изменении количества движения механической системы не характеризует вращательное движение механической системы, а только поступательное.
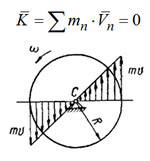
Приведен пример: Определить количество движения диска определенной массы, если известна его угловая скорость и размер.
Пример решения задачи на применение теоремы теоремы об изменении количества движения для определения скорости материальной точки
Лекция 3
Краткое содержание: Общие теоремы динамики точки. Количество движения точки. Элементарный и полный импульс силы. Теорема об изменении количества движения точки. Момент количества движения точки. Теорема об изменении момента количества движения точки. Работа силы. Мощность. Кинетическая энергия точки. Теорема об изменении кинетической энергии точки. Принцип Даламбера для материальной точки
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
Для решения многих задач динамики вместо непосредственного интегрирования дифференциальных уравнений движения оказывается более эффективным пользоваться так называемыми общими теоремами, которые являются следствием основного закона динамики.
Количество движения точки
Количеством движения материальной точки 


Количество движения точки в физике часто называют импульсом материальной точки.
Проекции количества движения точки на прямоугольные декартовы оси координат равны:


Рекомендуемые материалы
Единицей измерения количества движения в СИ является – 
Элементарный и полный импульс силы.
Действие силы 


Полный импульс силы 




В частном случае, если сила 


Проекции импульса силы на прямоугольные декартовы оси координат равны:


Единицей измерения импульса в СИ является – 
Теорема об изменении количества движения точки.
Теорема. Производная по времени от количества движения точки равна действующей на точку силе.
Запишем основной закон динамики 

Тогда 
что и требовалось доказать.
В проекциях на координатные оси уравнение (*) можно представить в виде:


Теорема импульсов (в дифференциальной форме). Дифференциал от количества движения точки равен элементарному импульсу силы, действующей на точку.
Умножим левую и правую части уравнения (*) на 

В проекциях на координатные оси получаем:



Теорема импульсов (в интегральной форме). Изменение количества движения точки за какой-либо промежуток времени равно импульсу силы за этот же промежуток времени.
Интегрируя обе части уравнения (**) по времени в пределах от нуля до 
В проекциях на координатные оси получаем:


Момент количества движения точки.
В некоторых задачах в качестве динамической характеристики движущейся точки вместо самого количества движения рассматривают его момент относительно какого-либо центра или оси. Эти моменты определяются также как и моменты силы.
Моментом количеством движения материальной точки 
Момент количества движения точки называют также кинетическим моментом.
Момент количества движения относительно какой-либо оси 


Если количество движения 






Единицей измерения количества движения в СИ является – 
Теорема об изменении момента количества движения точки.
Теорема. Производная по времени от момента количества движения точки, взятого относительно какого-нибудь центра, равна моменту действующей на точку силы относительно того же центра.
Доказательство: Продифференцируем момент количества движения по времени



что и требовалось доказать.
Теорема. Производная по времени от момента количества движения точки, взятого относительно какой-либо оси, равна моменту действующей на точку силы относительно той же оси.
Для доказательства достаточно спроектировать векторное уравнение (*) на эту ось. Для оси 
Следствия из теорем:
1. Если момент силы относительно точки равен нулю, то момент количества движения относительно этой точки величина постоянная.


2. Если момент силы относительно оси равен нулю, то момент количества движения относительно этой оси величина постоянная.


Работа силы. Мощность.
Одна из основных характеристик силы, оценивающих действие силы на тело при некотором его перемещении.
Элементарная работа силы скалярная величина равная произведению элементарного перемещения на проекцию силы на это перемещение.


Единицей измерения работы в СИ является – 
При 
Частные случаи:
Элементарное перемещение равно дифференциалу радиуса вектора точки приложения силы.
Элементарная работа силы равна скалярному произведению силы на элементарное перемещение или на дифференциал радиуса вектора точки приложения силы.
Элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки.
Если сила 



Работа силы на любом конечном перемещении 
Мощностью силы называется величина, определяющая работу, совершаемую силой в единицу времени. В общем случае мощность равна первой производной по времени от работы.

Мощность равна скалярному произведению силы на скорость.
Единицей измерения мощности в СИ является – 
В технике за единицу силы принимается 
Пример 1. Работа силы тяжести.




Тогда, 


Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной.
Пример 2. Работа силы упругости.
Рассмотрим материальную точку закрепленную на упругом элементе жесткости с, которая совершает колебания вдоль оси х. Сила упругости (или восстанавливающая сила) 




Работа силы упругости равна половине произведения жесткости упругого элемента на разность квадратов начального и конечного удлинения (или сжатия) упругого элемента.
Работа силы упругости равна площади фигуры (трапеции) расположенной под кривой 
Пример 3. Работа и мощность пары сил.




Мощность пары сил равна
Кинетическая энергия точки
Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.
Теорема об изменении кинетической энергии точки.
Теорема. Дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку.
Доказательство: Основной закон динамики 
Умножим левую и правую части уравнения скалярно на 




Теорема. Производная по времени от кинетической энергии точки равна мощности, подводимой к этой точке.
Теорема. Изменение кинетической энергии точки на каком-либо перемещении равно работе силы, действующей на точку на этом же перемещении.
Принцип Даламбера для материальной точки
Уравнение движения материальной точки относительно инерциальной системы отсчета под действием приложенных активных сил и сил реакции связей имеет вид:
Информация в лекции «18 Нечеткие множества» поможет Вам.



Силой инерции материальной точки называют произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е. 
Если использовать понятие силы инерции, то основной закон динамики принимает вид:
Принцип Даламбера. При движении материальной точки активные силы и силы реакции связей вместе с силой инерции точки образуют равновесную систему сил.
Принцип Даламбера называют еще методом кинетостатики. Задачи динамики с помощью этого метода сводятся к задачам статики.